Geometry - Area and surface
| © 2006 Rasmus ehf |
Geometry - Area and surface |
Lesson 6
Units of measurement for Area and Surface area
Units of measurement for Area:
| km2 | hm2 | dam2 | m2 | dm2 | cm2 | mm2 |
| 1 | 00 | 00 |
| 1 m2 = 100 dm2 = 10000 cm2 |
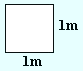 |
A = 1m × 1m = 1m2 |
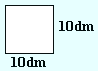 |
A = 10dm × 10dm = 100dm2 |
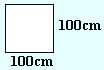 |
A = 100cm × 100cm = 10000cm2 |
You know how to find the area of a plane, for example:
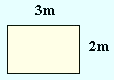
A = 3m × 2m = 6m2 six square metres.
If you are asked to give the answer in square centimetres, you can use the table below to help you convert the number.
| km2 | hm2 | dam2 | m2 | dm2 | cm2 | mm2 |
| 6 | 00 | 00 |
| 6m2 = 60000cm2 |
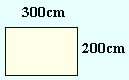
Another method is to change metres to centimetres before finding the area.
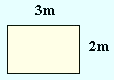 =
=
|
A= 300cm × 200cm = 60000cm2 |
Surface area
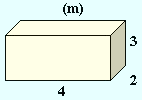
To find the surface area of a box you must find the area of each side or face of the box.
 |
|
3m × 4m = 12m2 |
|
|
2m × 3m = 6m2 | |
|
|
2m × 4m = 8m2 |
12m2 + 6m2 + 8m2 = 26m2
Here you see the area of three of the sides. But the box has 6 sides. Three more, the same as the ones above. The surface area of the box is therefore:
26m2 × 2 = 52m2
To find the surface area of an object, you need to find out the shapes of the faces and calculate their areas.
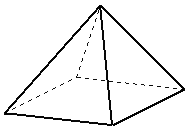
| Surface area of a pyramid = | area of a rectangle + the area of 4 triangles |
| Surface area of a pyramid = |  + + + + + + + + |
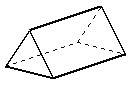
| Surface area of a prism = |
 +
+
 +
+
 +
+
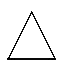 +
+
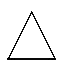 |
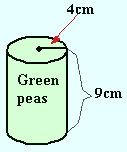
| Surface area of a can (cylinder) = |
 +
+
 +
+
 |
| Area of the top | |
| Area of the bottom | Same as top |
If the label is flattened out, it is in the shape of a rectangle.
 |
A = length × width = 9cm × 25.12cm = 226.08cm2 |
| This
side is the circumference
of a circle. |
| Surface area of a can (cylinder) = |
 +
+
 +
+
 |
| A = | 50.24cm2 + 50.24cm2 + 226.08cm2 = 326.56cm2 |
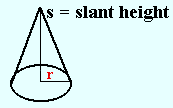 |
Surface area of a cone Area of the top |
|
| Area of the bottom |
|
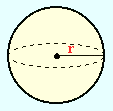 |
Surface area of a sphere = |
|
Practice these methods and then try Quiz 6 on Area. Remember to use the Checklist to keep track of your work.