A Review of Algebra
| © 2004 Rasmus ehf |
A Review of Algebra |
Here are some typical algebra problems that you might find on final grade exams. See the suggested topic areas on the Rasmus-Math web for more practice.
Problem 1: Expand the powers and simplify the expression.
6² + 2×2³=
36 + 2×8=
36 + 16 = 52
Problem 2: Simplify.
y + xy +2y= 3y + xy
Problem 3: Simplify.
xy +yx = 2xy
Problem 4: Simplify.
a×ab = a²b
Problem 5: Simplify.
![]()
Problem 6: Factorise and simplify:
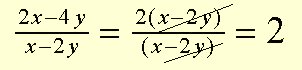
See Factorising expressions and Multipying and dividing fractions
Problem 7: Expand and simplify:
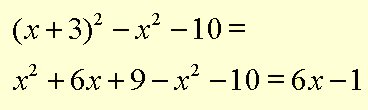
Problem 8: Solve for x:
x +14 = 30
x = 30 - 14
x = 16
Problem 9: Solve for x:
![]()
![]()
Then x = 72
Problem 10: Solve for x:
5(x + 2) = - (8 - 3x)
5x + 10 = - 8 + 3x
5x -3x = -8 -10
2x = -18
x = -9
Problem 11: Find the value of the expression if a = 3.
7a - (2a)² =
7×3 - (2×3)² =
21 - 6² =
21 - 36 = -15
Problem 12: Simplify as much as possible:
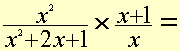
|
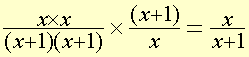
|
See Mutiplying and dividing fractions and Factorising
Problem 13: Simplify as much as possible:
|
|
|
|
See Adding and subtracting fractions
Problem 14: Solve the equation.
|
|
|
|
|
|
|
|
|
|
|
|
Problem 15: Factorise the expressions and find values for x and y given that they are both whole numbers.
Method 1:
x² - y² = 15 See Factorising expressions and Ordered pairs
(x - y)(x + y)=3×5
This gives two equations.
a) x - y = 3
b) x + y = 5 Add the equations to get:
x + x + y - y = 3 + 5
2x = 8 so x = 4
Substitute the value for x in one of the equations to get:
4 + y = 5
y = 5 - 4
y =1
Method 2:
x² - y² = 15
(x - y)(x + y)=1×15
This gives two equations.
a) x - y = 1
b) x + y = 15 Add the equations to get:
x + x + y - y = 1 + 15
2x = 16 so x = 8
Substitute the value for x in one of the equations to get:
8 + y = 15
y = 15 - 8
y = 7
If you have done all the previous quizzes and have prepared yourself well, try your luck on the Final quiz!