Fractions - Adding and subtracting
| © 2006 Rasmus ehf |
Fractions - Adding and subtracting |
Lesson 3.
1. First check to see if the fractions have a common denominator.
Find a common denominator by multiplying the numerator and denominator of each fraction by the factor(s) needed.
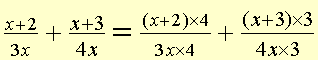
| 3x has the factors 3 and x, 4x has the factors 4 and x, | |
| the common denominator has the factors | 3×4×X |
Next work with the numerators.
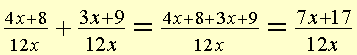
Collect like terms and simplify. Note that 4x+3x=7x and 8+9=17
2. Sometimes you have to write numbers in a different way .
Example:
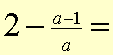
| The whole number 2 can be written as the fraction | 2/1 |
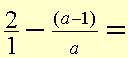 It
pays to put the term above the dividing line in brackets because of the negtive
sign in front of the fraction.
It
pays to put the term above the dividing line in brackets because of the negtive
sign in front of the fraction.
Find the common denominator.
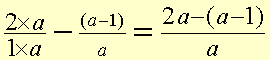
Remove the brackets being careful to change the signs of the terms in brackets.
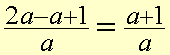
Then collect like terms and simplify.
3. A more complicated example.
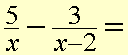
Somtimes there is no common factor in the denominators
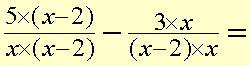
Then you multiply the denominators to get the common denominator x(x-2). Simplifying we get
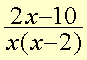
You have to take care when working with algebra fractions. The denominator x(x-2) cannot be equal to 0 because you cannot divide by zero.
| Therefore |
|
| Therefore |
|
| and |
|
| The sign |
|
means is not equal to |
4. Multiplying brackets.
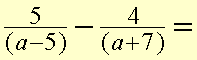
Multiply by the denominators to make the denominator the same.
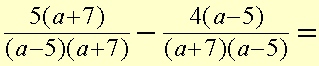
Expand the expression by multiplying out of the brackets in the numerator.
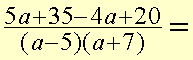
Then collect like terms and simplify.
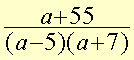
In this example, the variable a may not have the values +5 or -7 because you cannot divide by zero.
Try Quiz 3 on Fractions. If you score higher than 80%, look in the mirror and say to yourself: "You are very good at algebra!"