Fractions × and ÷
| © 2006 Rasmus ehf |
Fractions × and ÷ |
|
Lesson 1.
Factorising and simplifying fractions
Let's review factorising.
In the example 6 = 2 × 3, we say that the number 6 has the factors 2 and 3. All whole numbers can be written as a product of two or more numbers, which are called factors. A number with only two factors, 1 and the number itself, is a prime number (2, 3, 5, 7, 11, 13, 17, 19, 23, . . . ).
Sometimes letters are used to represent numbers, which are called variables. We can still find the factors by expanding the term.
Example:
Multliplying a number by 1 does not change its value, therefore it is not considered a factor when factorising.
Remember that a horizontal line (bar) is the sign for division.
How to use common factors to simplify fractions.
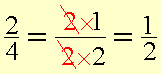We see that 2 = 2×1
and 4 = 2×2
The number 2 is a common factor ( 2÷2 = 1). We can simplify the fraction by cancelling out the common factor.
To reduce a fraction to lowest terms, divide both numerator and denominator by their common factors.
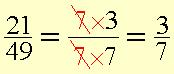We see that 21
= 7×3 and 49 =
7×7 .
The number 7 is a common factor. We can reduce the fraction by cancelling out the common factor.
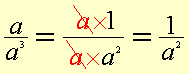We
see that
and
.
The variable a is a common factor. We can reduce the fraction by cancelling out the common factor.
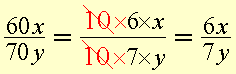We see that 60 =
10×6
and 70 = 10×7 .
The number 10 is a common factor. We can reduce the fraction by cancelling out the common factor.
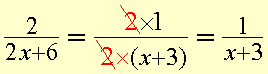Begin by factorising. ( 2x + 6 ) = 2(x + 3)
The number 2 is common to both the numerator and the denominator. We reduce the fraction by cancelling the common factor (2) from both the numerator and the denominator.
Prime numbers can only be divided by
1
and themselves.
Therefore, there is no common factor and the fraction can not be simplified.
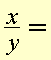Unlike variables. They can only
be divided by 1 and themselves.
Therefore, there is no common factor and the fraction can not be simplified.
Try Quiz 1 on Multiplying and dividing fractions. Remember to use your Checklist.