Lesson 5

Pythagoras' Rule

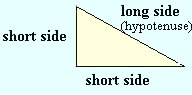The Greek mathematician Pythagoras was one of the first to prove that for right-angled triangles, the sum of the squares of the 2 shorter sides equals the square of the longest side of the triangle (hypotenuse).

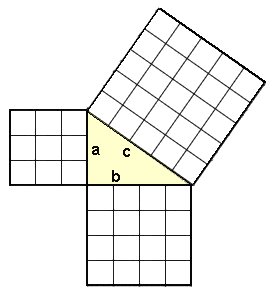
In the diagram below, squares are drawn on the sides of a right-angled triangle. The area of the squares show the value of the squares of the sides (a, b, c). If you count the number of little squares for each side, you see that the sum of the squares on the shorter sides a and b is 25, the same as for side c.

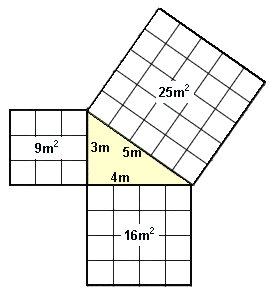
The lengths of the sides and the areas of the squares are shown below. 

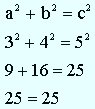
Example:

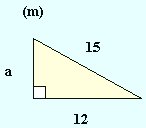
How long is side a? 

    Using Pythagoras's rule : 

   Check the result:  (substitute 9 for a)      

Practice these methods and then try Quiz 5 on Area. Remember to use the Checklist to keep track of your work.