© 2006  Rasmus ehf og Jóhann Ísak Pétursson

Fractions of fraction  

Lesson 2

Let’s look at more complicated examples.

Example 1

 

We can multiply both the numerator and denominator by -1 without changing the fraction. 

If we multiply the  the denominator by -1 it will be the same expression as the numerator. We leave the -1 in the numerator outside the bracket and cancel .

 

We can summarise the results of the above example by the simple rule:

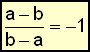This rule applies if we have a fraction where the numerator and the denominator are the same except that all the terms in the numerator have the opposite sign to the terms in the denominator .
 
Example  2

We add together the terms in the numerator by finding the common denominator. We do the same with the denominator.

Now we can change the division into a multiplication as before and put the two fractions together over one dividing line.

 Finally we can factorise and cancel out the common factors

Example 3

Again we add together the terms in the numerator and the denominator.

Next put the two fractions together over one dividing line.

Then we simplify, factorise and cancel out the common factors.

 

Note:   −5(x − 4) = 20 − 5x.

Sometimes it’s simpler to multiply the numerator and the denominator with the commom denominator of all the fractions.

Example 4

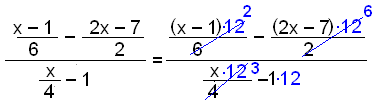The common denomiator of all the fractions in this example is 12.

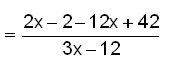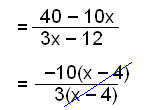We multiply every term by 12, cancel out the fractions and then multiply out of the brackets.
Finally we factorise and cancel as much as possible.
 

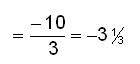Try Quiz 2 on Fractions dividing fractions. Remember to use your Checklist.