© 2008 Rasmus ehf og Jóhann Ísak Pétursson
|
© 2008 Rasmus ehf og Jóhann Ísak Pétursson |
Sequences and Series |
|
Geometric Progression GP
A sequence in which each term is a fixed multiple of the previous term is called a geometric sequence or Geometric Progression ( GP ). In other words there is always the same ratio between consecutive terms.
![]()
where k is a fixed number. For example in the sequence 100, 50, 25, 12½, 6¼, 3⅛, . . . . k equals a half.
Remember the dots show that this is an infinite sequence.
If we write this sequence term by term we can see the rule for the n th term:
a1 = 100
a2 = 100∙½ = 50
a3 = 100∙(½)2 = 25
a4 = 100∙(½)3 = 12½
a5 = 100∙(½)4 = 6¼
![]()
![]()
![]()
an = 100∙(½)n-1
The following rule holds for a GP:
|
an = a1∙kn-1 |
The first two terms in a GP are 8 and 6. Find the first four terms of the sequence.
First we find the ratio k.
![]()
Now we can find the third and fourth terms.
a1 = 8
a2 = 8∙¾ = 6
a3 = 8∙(¾)2 = 4½
a4 = 8∙(¾)3 = 3⅜
The third and fourth terms in a GP are 2 and 4. Find the first six terms.
First find the ratio k.
k = 4/2 = 2
We use this value of k and one of the given terms , for example a4 , in the rule for a GP to find a1
a4 = a1∙k3
4 = a1∙23 = a1∙8
a1 = 4/8 = ½
Now it's easy to find the rest of the sequence:.
a2 = ½∙2 = 1
a3 = ½∙22 = 2
a4 = ½∙23 = 4
a5 = ½∙24 = 8
a6 = ½∙25 = 16
In a GP a3 = 128 and a6 = 2. Find the first six terms.
We need to multiply a3 = 128 three times by k to get a6 = 2.
128∙k3 = 2
k3 = 2/128 = 1/64
![]() =
¼
=
¼
Now we can use the rule to find a1.
a3 = a1∙k2
128 = a1∙(¼)2
a1 = 128/(¼)2 = 128∙16 = 2048
The rest of the sequence follows.
a2 = 2048∙¼ = 512
a3 = 2048∙(¼)2 = 128
a4 = 2048∙(¼)3 = 32
a5 = 2048∙(¼)4 = 8
a6 = 2048∙(¼)5 = 2
Given a GP with a3 = 250 and a5 = 62½. Find the ratio k and the first four terms.
We need to multiply 250 twice (5 – 3 = 2) by k to get 62½.
250∙k2 = 62½
k2 = 62½/250 = ¼
k = ![]() ½
½
In this case there are two possible values for k, a positive and a negative. We find a2 by dividing by k and a1 by dividing by k2 which is always positive.
a2 =
250/(![]() ½) =
½) =
![]() 500
500
a1 = 500/½ = 1000
This means we get two possibilities for all the even numbered terms in the sequence.
a1 = 1000
a2 =
![]() 500
500
a3 = 250
a4 = ![]() 125
125
Now let's look at further examples of sequences that obey the rule an = a1∙kn−1.
Look at the example.
a1 = 12
a2 = 3
a3 = 0.75
a4 = 0.1875
a5 = 0.046875
We see that k = 3/12 = ¼ and the terms decrease rapidly. The sequence can be shown graphically .
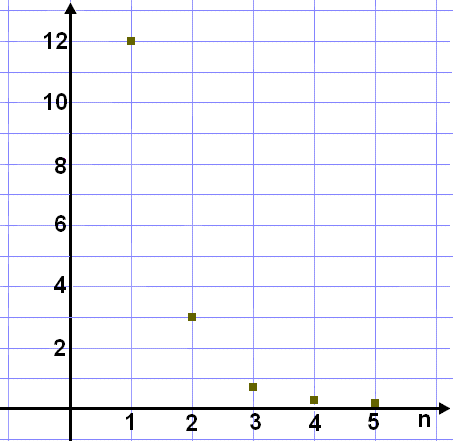
As n gets bigger the numbers get rapidly nearer and nearer to zero. The n axis is a horizontal asymptote. Sequences that behave in this way are called convergent sequences. This sequence converges to zero.
A GP is convergent if the ratio k is between 1 and -1 because multiplication by k makes each term smaller than the previous term and eventually tends to zero.
|
Rule: A GP is convergent if −1 < k < 1 |
A sequence of numbers where each number is a percentage of the previous number
is a GP. An increase of 10% means an increase from 100
to110 so the ratio for a sequence with
a 10% increase between terms is k = 110/100 = 1.1. In the same way,
a decrease by 10% means that 100 decreases to 90 so that the ratio k =
90/100 = 0.9.
Here is a list of values of k for different percentages.
1% increase, k = 1.01
5% increase, k = 1.05
10% increase, k = 1.10
25% increase, k = 1.25
90% increase, k = 1.90
100% increase, k = 2.00
200% increase, k = 3.00
In general:
|
p% increase, k = (1 + p/100) |
|
p% decrease, k = (1 − p/100) |
Steve paid 3000 pounds for a car. He borrowed the money at 10 % annual
interest without having to repay the loan for five years. The value of the car
decreases by 20% each year. How much did it cost Steve to own the car at the end
of the five year period if other costs are ignored?
First look at the increase because of the interest he has to pay on the loan.
Original loan, a0 = 3000 pounds.
After 1 year, a1 = 3000∙1.10 = 3300 pounds.
After 2 years, a2 = 3300.∙1.10 = 3630 pounds.
After 3 years, a3 = 3630.∙1.10 = 3993 pounds.
After 4 years, a4 = 3993.∙1.10 = 4392 pounds.
After 5 years, a5 = 4392∙1.10 = 4831 pounds.
Total interest:
4831 – 3000 = 1831 pounds.
Devaluation of the car:
Original value a0 = 3000 pounds.
After 1 year, a1 = 3000∙0.80 = 2400 pounds.
After 2 years, a2 = 2400∙0.80 = 1.920 pounds.
After 3 years, a3 = 1920∙0.80 = 1.536 pounds.
After 4 years, a4 = 1536∙0.80 = 1.228 pounds.
After 5 years, a5 = 1228∙0.80 = 983 pounds.
Total loss:
3000 – 983 = 2017 pounds.
Total cost 1831+ 2017= 3848 pounds
From the above example
we see that when we can calculate compound interest by using the rule an = a1∙kn−1
but we need to take care to remember that a1 represents the
value with interest after the first year.
If, however we use a0 to represent the original loan or capital then the formula is:
|
an = a0∙kn |
We can also use this formula for decreases in value, in which case k < 1.
Sally deposites 100 pounds in a bank that pays 8% annual interest. How much will she have after 10 ár?
We use the rule a10 = a0∙k10 where a0 = 100 and k = 1.08
a10 = 10.000∙1.0810 = 216 pounds.
Sally knows of another bank that pays 10% annual interest. If she deposites money in this bank how long will it take to double in value?
2 = 1∙1.10n
Here we need to use logs to find the index n..
ln 2 = ln 1.1n
|
ln 2 = n∙ln 1.1 |
Using the rule ln an = n∙ln a |
n = ln 2 / ln 1.1 ≈ 7.3 years.
Practise these methods then try
Quiz 2 on Sequences and Series
Remember to use the checklist to keep track of your work.