© 2010  Rasmus ehf  and Jóhann Ísak

Integration

Lesson 4

Volumes of revolution

Imagine that the graph of the function y = f(x) is rotated once about the x - axis ( or y - axis ) so that we have a 3 - dimensional solid.
The object  could look something like the diagram below and is called a solid of revolution.

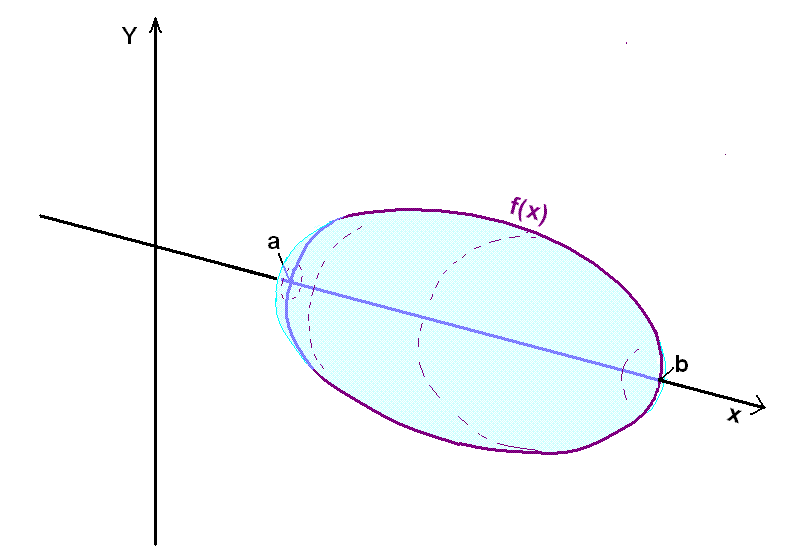
We are going to see how integration can be used to find this type of volume, called a volume of revolution. When we first tried  to find the area under a graph we divided the area into small strips, each with the height  f(x) and then added the area of these strips together. To find the volume formed when we rotate a curve about the x axis  we divide the solid into small  discs with radius f(x) ( see the diagram below ).

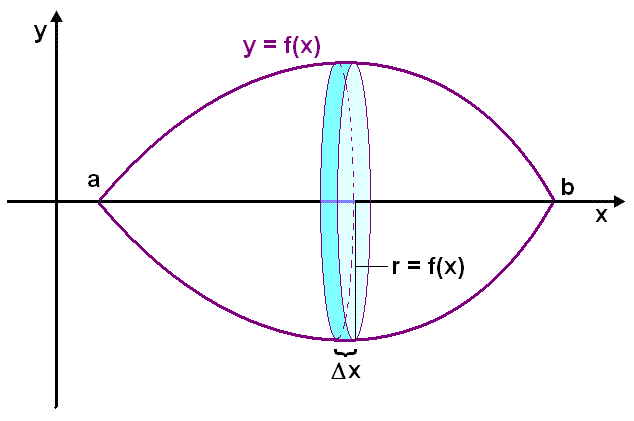
The thickness of each disc is  x and the surface area  A. The discs are cylindrical so we can use the formula for the volume of a cylinder, Volume R = r²·h.  In this case the height is  x and radius of the surface is f(x) so the volume of each disc is

   R = r²·x = (fx)²x

We now sum the volumes of the discs using integration, with the boundaries x = a to x = b.

It's easiest to take outside the integration sign as it's a constant, and then multiply with after integrating.

Example 1

Find the volume of the solid  formed when the graph of   is rotated once round the x - axis .

This is what the graph looks like.

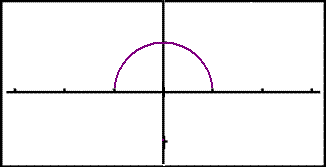This is  obviously the graph of a semicircle with radius one unit. So, when we rotate this about the x -  axis we get a sphere also with radius one unit. To find the volume we use the  formula :

    on the interval  –1 ≤ x ≤ 1.

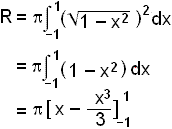
       = p(1 – ⅓ – (–1 – (–⅓)))

       = p(1 – ⅓ + 1 – ⅓)

       = 4/3

Let's continue with this example and find a formula for the volume of a sphere with radius r.

In this case we rotate  , which is a semicircle with radius r, about the x  - axis..

The calculations follow:

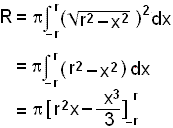     s

       = p(r³ – ⅓ r³ – (–r² – ⅓(–r³)))

       = p(r³ – ⅓ r³ + r³ – ⅓ r³)

       = pr³(2 – ⅔)

       = 4pr³/3

This is a formula that you will easily recognise from geometry. Many proofs of this sort in geometry can be accomplished using integration.

Example 2

A ring has a straight sided inside surface and a curved outer surface. The radius of the inner ring is  8 mm and the outer surface is part of the parabolic curve  
f(x) = 6x – x² on the interval 2 ≤ x ≤ 4. Find the volume of the ring .

We start by looking at the graph of the line y = 8  and the parabola f(x) = 6x – x² . The shaded area between these two graphs are a cross section of the ring.

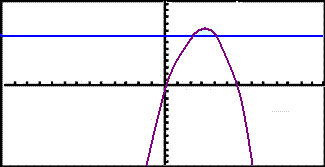Rotating this cross section around the x - axis shows us the whole ring.

First calculate the points of intersection:

   6x – x² = 8

            0 = x² – 6x + 8

               = (x – 2)(x – 4)

The graphs intersect in  x = 2 and x = 4.

The parabola is the upper function so we first calculate the volume of the outer ring  and then subtract the volume of the inner ring on the interval  2 ≤ x ≤ 4.

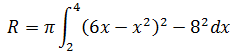
   (6x – x² )²– 8² = (6x – x²)(6x – x²) – 64

                         = 36x² – 6x³ – 6x³ + x⁴

                         = x⁴ –12x³ + 36x² – 64

The area is:

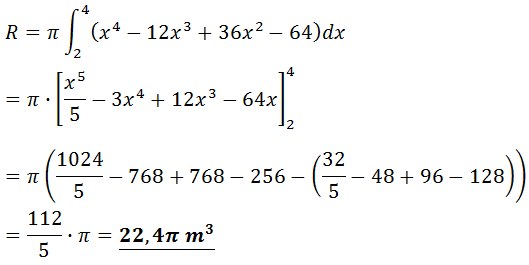
Example 3

Find the volume of the cone that is formed when the line  y = x is rotated once about the  x-axis on the interval x = 0 to x = 4 (see diagram).

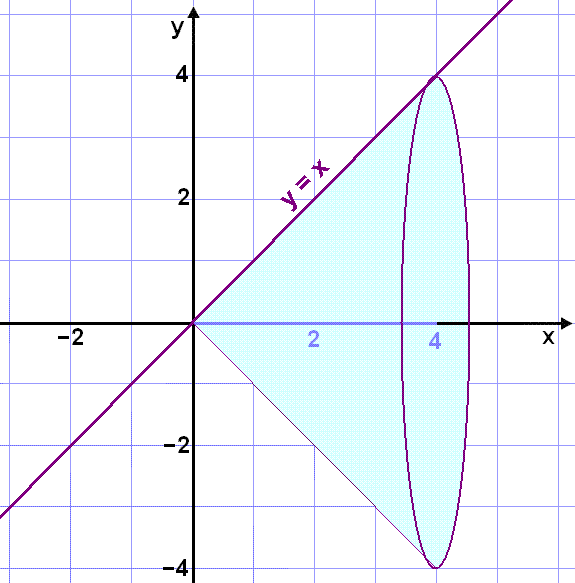
   R = ⅓ 4³ =64/3

It would perhaps be more natural to see the cone standing vertically, symmetrical about the y - axis rather than the x - axis.

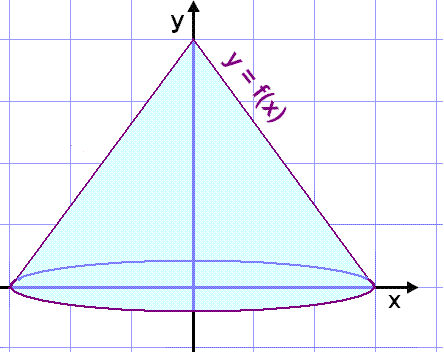
In that case we could use another method to find the volume forming the cone  by rotating the line  y = f(x) once about the y - axis.  Imagine cutting a thin cylinder or tube out of the cone as shown in the diagram and opening it out to form a rectangle.

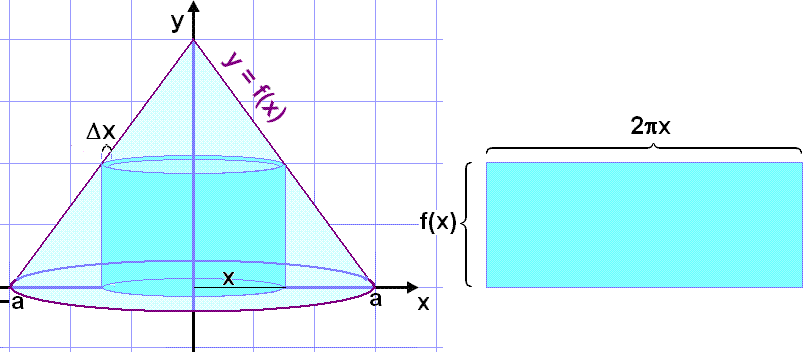
This method is often simpler to use than the previous method as it does not involve squaring the function.

Example 4

Find the volume of the bell shaped solid of revolution when the curve given by the function f(x) = 4 – x² is rotated once about the y-axis. The diagram below shows the shape of the solid. 

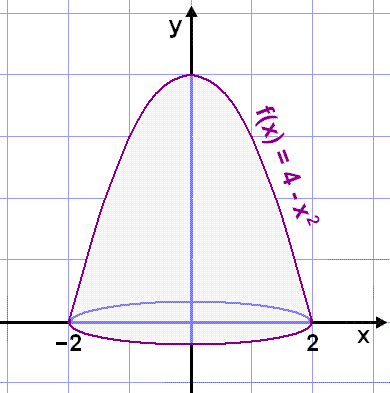
Using the second method, the cylinder method, we get that the volume is:

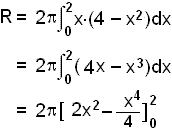
       = 2(8 – 4) = 8

Example 5

Find the volume of the cone formed when the line  y = 2x + 1 with 0 ≤ x ≤ 4 is rotated about the y-axis.

The diagram is shown here.

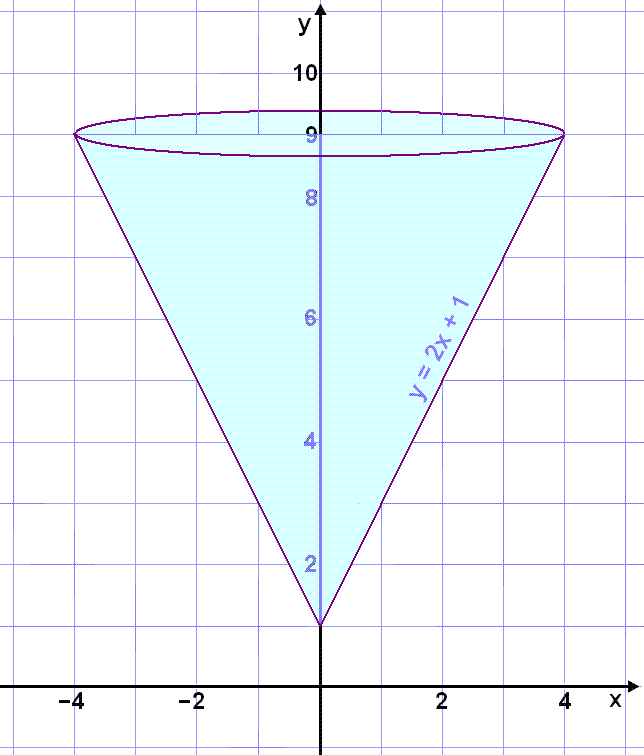
If we use the second method with  x = 0 to x = 4 we get the volume of the solid that lies outside the cone so we need to subtract f(x) from 9. The volume is then:

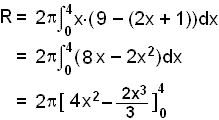
      = 2(64 – 42⅔) = 128/3

Example 6

A glass solid is formed by rotating the area between the parabola  f(x) = x²/10 and the line  y = x + 20 about the y - axis . Find the volume of revolution.

First, a diagram.

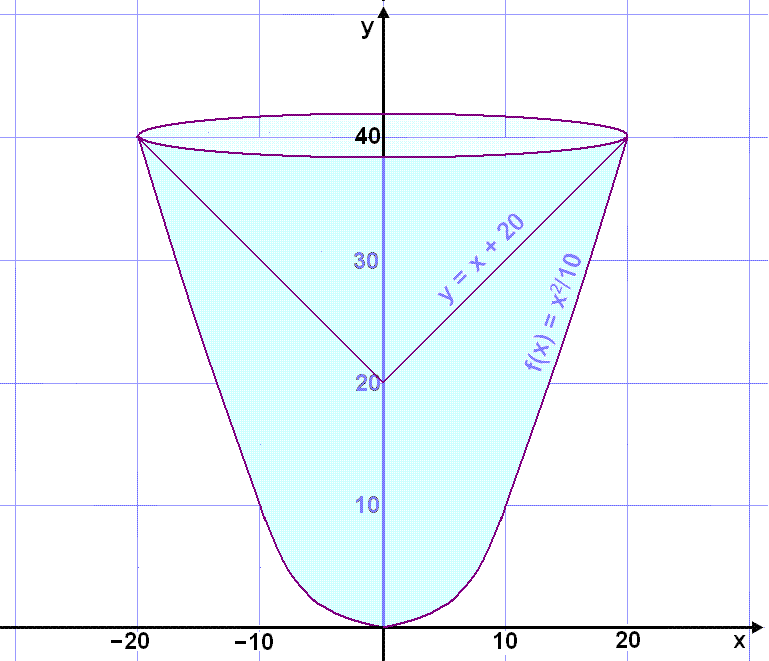
The curves intersect where x = 20 so  we can subtract the lower function from the upper function as in example 5 and use the formula on the interval x = 0 to x =  20

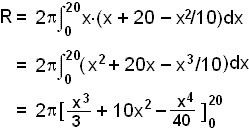
      = 2(2666⅔ + 4000 – 4000) = 16000/3 .

Practise these methods then take  test 4 on integration.

Remember the check list!!