Integration
| © 2010 Rasmus ehf and Jσhann Νsak |
Integration |
|
Lesson 3
Areas between the graphs of functions
Areas bounded by the graphs of functions can be found by integration. For
example we will find the area bounded by the two graphs f(x) = x2 + 5x 3
and y = x.
This is the area shown in the calculator:
 |
 |
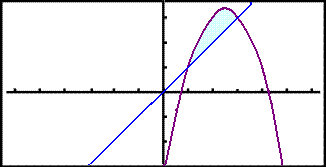We begin by finding the points of intersection of the two graphs to give us the boundaries of the area:
x2 + 5x 3 = x
x2 + 4x 3 = 0 Simplify.
(x2 4x + 3) = 0 Take 1 out of a bracket.
(x 1)(x 3) = 0 Factorise.
(x2 4x + 3) = 0
(x 1)(x 3) = 0
The points of intersection are x = 1 and x = 3. They lie on the line y = x so the y coordinates are the same as the x coordinates, i.e. (1, 1) and (3, 3).
We only need to use the x coordinates to calculate the area between each curve and the x - axis.
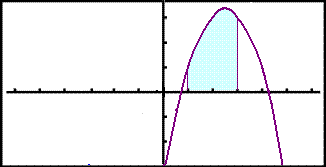
The integral 
gives the area
between the x - axis and the function
f(x) = x2 + 5x 3 on the interval 1 to 3.
This is the shaded area of the graph below
In the same way
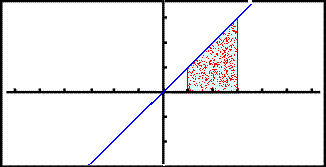
is the area
between y = x and the x - on the same interval. Again the graph shows the area
found.
If we put these two graphs together we see that the area we want to find is the difference between the two above.
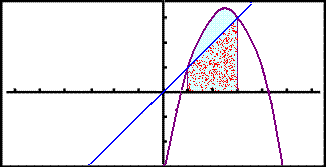
So we simply have to take the difference between the two integrals to find the area we require.
 |
|
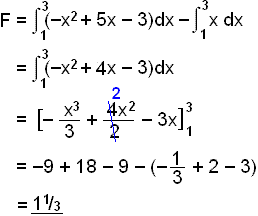The new equation of the parabola will be f(x) = x2 + 5x 3 2 = x2 + 5x 5 and of the line y = x 2. The diagram shows the new situation.
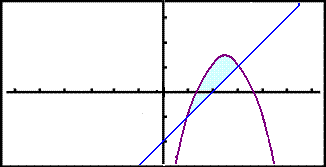
The points of intersection remain the same as we have added 2 to both sides of the equation. Below are the calculations if you are not convinced!
x2 + 5x 5 = x 2
x2 + 4x 3 = 0 Simplify.
(x2 4x + 3) = 0
(x 1)(x 3) = 0 Factorise.
Again the solutions are x = 1 and x = 3. Integrating in the same way you can see that the 2 again simplifies out so we have the same result as before.
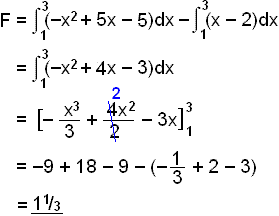
This means that when calculating the area between curves we do not need to worry about whether the area is above or below the x - axis, the method is always the same.
|
The area bounded above by the graph of f(x) and below by the graph of g(x) is:
The bounds x = a and x = b are the solutions of the equation f(x) = g(x) |
Example 1
Find the area between the parabola f(x) = x2 4 and the line y = x 2.
We begin by solving the equation x2 4 = x 2 to find the area boundaries
x2 4 = x 2
x2 4 x + 2 = 0
x2 x 2 = 0
(x + 1)(x 2) = 0
The solutions are x = 1 and x = 2.
It's a good idea to look at the graph and the area in involved in the calculator.
|
|
 |
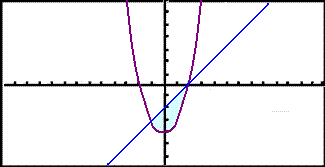We see that the line bounds the area above so we subtract the integral of the parabola from that of the line.
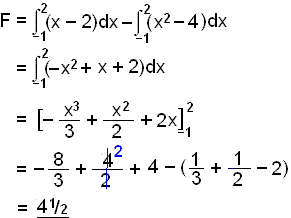
Example 2
Find the area enclosed between the graphs of f(x) = sin x and g(x) = cos x
on the interval 0 ≤ x < 2p
The calculator shows us the area we are going to find.
|
|
 |
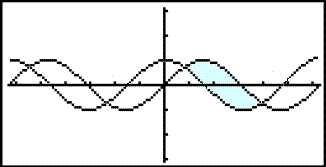Again we have to start by finding the points of intersection of the two graphs.
Solving the equation sin x = cos x.
sin x/cos x = 1 Divide through by cos x
tan x = 1
x = tan1
1 = 
/4
+ n·
This means
that x = /4
and x = 5/4
on the interval 0 ≤ x < 2
The graph of f(x) = sin x lies above the graph of g(x) = cos x on all of the interval between the points of intersection so the area calculations are as follows:
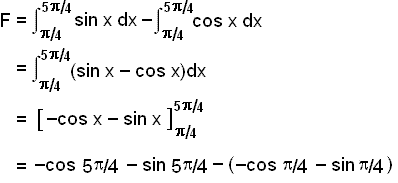
Now
cos
/4
= sin /4
=
and cos 5/4
= sin 5/4
= 
.
The exact value of the area is therefore
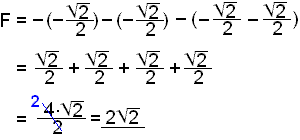
Example 3
Find the area bounded by the graphs of the straight line y = 3x + 1 and the polynomial f(x) = ⅓ x3 2x2 + 3x + 1.
First the graph is drawn with calculator help. The following window values should work
|
|
 |
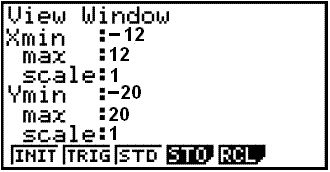Here is the graph:
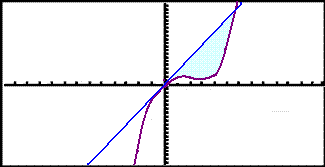
Now calculate the points of intersection.
⅓ x3 2x2 + 3x + 1 = 3x + 1
⅓ x3 2x2 = 0
x2 (⅓ x 2) = 0
The solutions are x = 0 and x = 6 bounds we need. The line is the upper function.
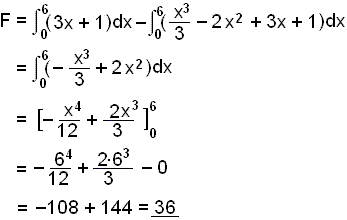
You can check your answer in the calculator (with RUN, OPTN, F4 and F4).
Practise
these methods then take test 3 on integration.
Remember the check list!!
