© 2009  Rasmus ehf    & Jóhann Ísak

Derivatives

Lesson 5

The Chain Rule

Example 1

Differentiate  f(x) = (x³+1)².

The only way we have of doing this so far is by first multiplying out the brackets and then differentiating. If we do this we get

f(x) = x⁶ + 2x³ +1 and therefore f´(x) = 6x⁵ +6x².

This is no problem with a simple example such as the one above but what happens if we have for example f(x) = (x³+1)⁶ ?
In this case it takes far too much effort to multiply out the brackets before differentiating.

To differentiate composite functions like this we use what is called the Chain Rule. We'll do example 1 again to see how it works.
 

f(x) is an example of a composite function as was introduced in functions 2.
It can be written as f(u) = u² where u = x³+1,  u is a function of x, that is u(x) = x³+1.

The Chain rule says that we first differentiate f(u) regarding u as the variable and get f´(u) = 2u ( just as (x²)´ = 2x )
Next we differentiate u and get  u´(x) = 3x².  Finally we multiply the two results together and get 
f´(x) = 2u·3x². Putting back the value of u we get  f´(x) =2 ( x³+1)·3x² =  6x⁵ +6x²

^{This gives us a rule called the Chain Rule which says that}

We have only stated the rule here but it can easily be proved for all continuous, differentiable functions.

Example 2

Differentiate the composite function f(x) = sin²x.

The notation sin²x is another way of writing  (sin x)² so that the square is the outer function and sin x the inner function. To begin with we will split this into two parts but with practice that will not be necessary. 

f(x) =  (sin x)²    can be written as f(u) = u² where u = sin x. 

 f´(u) = 2u  and u´= cos x  so that  multiplying together we get

   f´(x) = 2u·cos x = 2 sin x cos x

The Chain Rule states that to differentiate a composite function we differentiate the outer function and multiply by the derivative of the inner function.

Example 2 +

Differentiate f(x) = sin x².  This can  be written as f(u) = sin u where u = x²

So in this case sine is the outer function and the square is the inner function

   f´(x) = cos x² · 2x

Example 3

We can use the rules cos x = sin (/₂– x) and sin x = cos(/₂ – x) to find the derivative of cos x. 

   cos x = f(x) = sin (/₂ – x)

The derivative of sine, the outer function  is cos and the derivative of (/₂ – x), the inner function is –1 so we get

   f´(x) = cos(/₂ – x)·(–1)

          = sin x · (–1)

          = – sin x

Example  4

Find the derivative of f(x) = sin²x².

This can be written as f(x) = (sin x²)² so we have a triple composite function. The outermost function is a quadratic, then a sine and finally another quadratic.

We can write f = u² , where u = sinv and v = x² . Differentiating each function and multiplying together gives us 2 u· cos v · 2x, and putting back the values of u and v we get the result:

Example 5

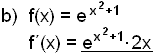Differentiating the exponential function leaves it unchanged ,the derivative of x2 + 1 is 2x.

Now we wish to find a rule for differentiating  f(x) = ln x.

We use a method called implicit differentiation which means differentiating both sides of an equation.

If f(x) = ln x then e^f(x) = x. If we differentiate both sides of the equation we get the following;

   e^f(x) = x

   e^f(x)·f´(x) = 1                Using the Chain Rule.

Solving for f´(x) we get

   f´(x) = 1/e^f(x)

          = 1/x                Remember x = e ^f(x).

Now we can find the derivative of other logarithmic functions.

Find the derivative of f(x) = log x.

First we have to remind ourselves of the logarithm rules and the relation between logs with different bases.  This is the rule we need:

In this way we can rewrite any logarithm as a natural logarithm, ln x.

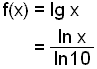
The logarithm ln 10 is a constant that has no effect on the derivative , the rest is easy.

Similar calculations work for any log function so we can summarise the following three rules:

 

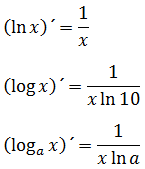Example 6

Differentiate f(x) = ln(x² + 1).

Example 7

Differentiate f(x) = x·ln x – x + 5.

   f´(x) = 1·lnx + x·1/x – 1 = ln x

Summarising derivatives

Derivative:

       k´ = 0           k = constant          x´ = 1

      (xⁿ)´ = nx^n–1    n can be any real number.

      (e^x)´ = e^x

      (a^x)´ = a^x · ln a

      (sin x)´ = cos x

      (cos x)´ = –sin x

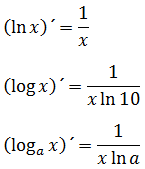
 Rules:

        (uv)´ = u´v + uv´

        (f(g(x))´ =  f´(g(x))·g´(x)

Practise these methods and then take test 5 on derivatives.

ps. Remember your check list.