© 2009 Rasmus ehf & Jóhann Ísak
|
© 2009 Rasmus ehf & Jóhann Ísak |
Derivatives |
|
Differentiating polynomials
The slope of a tangent varies, depending on the formula for the function, usually called f(x) and the point at which the tangent touches the curve.
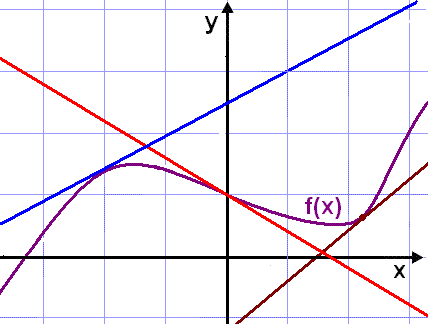
Three different tangents in three different colours have been drawn in the above diagram. The red tangent, for example, touches the graph of f(x) in just one point, (0,1). The gradient of the tangent is found by working out the average rate of change or gradient on an infinitely small interval around the point (0, 1).
We are now going to find a general method or formula for finding the gradient in any point of a function. This formula, or new function, is called the derivative of the original function. When we find it we say that we are differentiating the function. The derivative of f(x) is written using an apostrophe after the f. The notation is f´(x) or y´ The notation dy/dx is also commonly used.
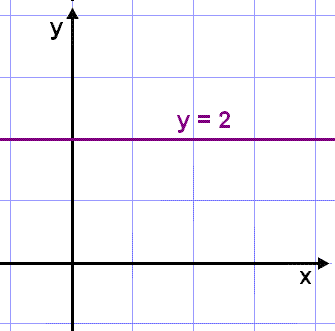
First look at the constant function, or f(x) = k where k is a constant value, for example f(x) = 2 or y = 2 The graph is shown here.
 |
 |
In this case it's difficult to talk about a tangent as the graph itself is a horizontal line. The gradient of the line is obviously 0 so we can say that if f(x) = 2 then f´(x) = 0. This is true of all constant functions, their graphs are horizontal lines and have gradient 0.
The rule is: if f(x) = k then f´(x) = 0.
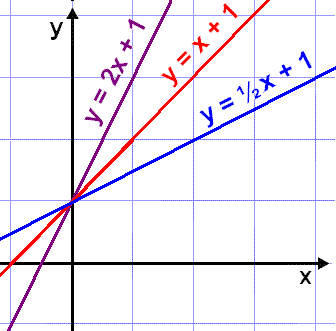
The second diagram shows three straight lines with different gradients. The derivative of a function is the gradient and therefore we get the following results:
y = 2x + 1 has the gradient 2 therefore y´
= 2
y = x + 1 has the gradient 1 therefore y´ = 1
y = ½x + 1 has the gradient ½ therefore y´ = ½
All first degree functions have straight line graphs and therefore we conclude that if we differentiate functions of the form f(x) = ax + b we get f´(x) = a.
Next we will look at the quadratic function f(x) = x2.
We can find the derivative by finding the average rate of change in an infinitely small interval as we did in lesson 1.
The definition of a derivative is:
We calculate this using the function f(x) = x2.
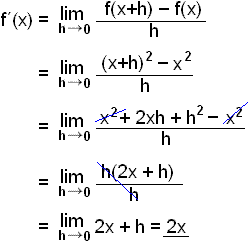 |
To find f(x+h) we put (x+h) into the formula for the function instead of x. |
Example 1
Differentiate the function f(x) = 2x2 + 4x.
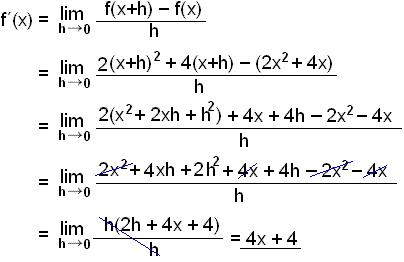
Note that if we differentiate 2·x2 we get 2·2x ( we found above that the derivative of x2 was 2x). The line y = 4x has the gradient 4 so the derivative of 4x is 4.
Adding these two results together gives us the result that the derivative of 2x2 + 4x is 4x + 4, the same result as before,
The following rule, which is easy to prove, applies to the addition of functions:
|
f(x) = ax2 + bx + c has the derivative f´(x) = 2ax + b. |
Example 2
Differentiate the function
![]() .
.
Instead of dividing by 2 we can think of this example as multiplying each term by ½ and we can therefore apply the above rules. Note that they only apply when dividing by a constant number. Notice also that the constant ¼ has the derivative 0 the same as any other constant.
![]()
Cancelling to simplify we get
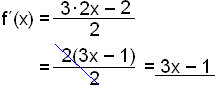
Example 3
Differentiate f(x) = x3. We have no rules so far for third degree functions so we have to use the definition:
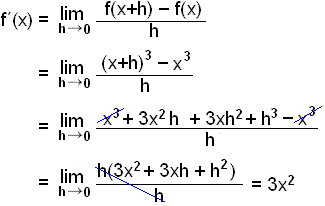
Example 4
Differentiate f(x) = x4.
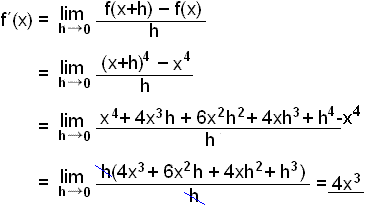
The above examples give us the following results:
f(x) = x0
has the derivative f´(x) = 0
f(x) = x1 has the derivative f´(x) = 1·x0
f(x) = x2 has the derivative f´(x) = 2·x1
f(x) = x3 has the derivative f´(x) = 3·x2
f(x) = x4 has the derivative f´(x) = 4·x3
In every case the result can
be obtained by multiplying by the original index or power and decreasing the
power by one.
This result can be shown to apply in general and we can write the following
rule:
|
f(x) = x n has the derivative f´(x) = n·x n–1 |
Example 5
Use the rules we have found to differentiate f(x) = x5 – 2x4 + 3x3 – 4x2 + 5x – 6.
f´(x) = 5x4
– 2·4x3 + 3·3x2
– 4·2x + 5 – 0
= 5x4 – 8x3 + 9x2 – 8x + 5
Example 6
Find the equation of the tangent to the curve f(x) = x5 – 5x3 + 4x in the point where x = 1.
We begin by finding the y value when x = 1.
f(1) = 1 – 5 + 4 = 0
The tangent is in the point (1, 0).
Next we find a formula for the gradient by differentiating the function.
f´(x) = 5x4 – 5·3x2 + 4
= 5x4 – 15x2 + 4
We can find the gradient when x = 1 by calculatingr f´(1).
f´(1) = 5 – 15 + 4 = –6
Using the formula for the equation of a straight line gives us the required equation.
y = –6(x – 1) + 0
y = –6x + 6

|
We can check our results by graphing the function and the tangent. The result is shown below. |
|
|
|
The equation of a tangent to the function f(x) in the point (a, f(a)) is y = f´(a)(x - a) + f(a) |
Practise these methods and then
take test 2 on derivatives.
ps. Remember your check list.