© 2008 Rasmus ehf og Jóhann Ísak
|
© 2008 Rasmus ehf og Jóhann Ísak |
Limits |
|
Limits and interval defined functions
What happens to the value of a function as x becomes infinitely large? Does the function also become infinitely large? Does it reach a maximum or minimum ? What in fact happens? That is what we are going to think about in the following text.
We know that we cannot divide by zero but what happens if we divide by a number very near to zero? We will see that sometimes the graph of the function goes up or down almost perpendicularly near this pont and sometimes the graph cannot go through the point leaving an infinitisimal hole.
Mathematics usues the concept of limits to consider problems of this sort.
Look at the function
![]()
The Casio calculator seems to draw a straight line when asked to graph this function (see the diagram). If you choose a large scale, such as INIT in V-Window you might notice a tiny break in the graph when x = 1. This is because, when x = 1 we are dividing by zero and the function is not defined in this point. The domain of the function is Df = R\{1}.
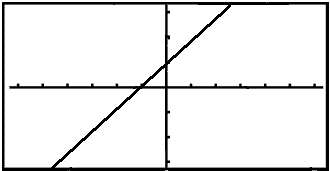
We will now try to work out what happens as x gets near to 1. This is written mathematically as follows:
![]()
Lim is the abbreviation of the latin word limes which means limit. The above notation means the value to which the function tends as x gets nearer and nearer to 1.
We can use algebra to simplify the function but must not lose sight of the original function and the problem of dividing by zero.
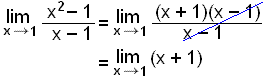
Now we no longer have the problem of dividng by zero so we can put the value x = 1 into the expression ( calculatef(1)).
![]() = 1 + 1 = 2
= 1 + 1 = 2
This shows us that the
function
![]() tends to the value 2 as x tends to 1.
tends to the value 2 as x tends to 1.
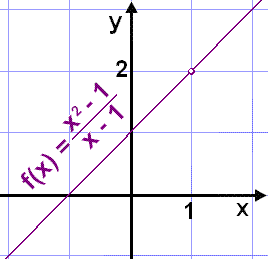 |
We can fill in this hole if we define a continuous function with the same algebraic expression but add a value that the function can take when x = 1. This new function g(x) is defined as follows: |
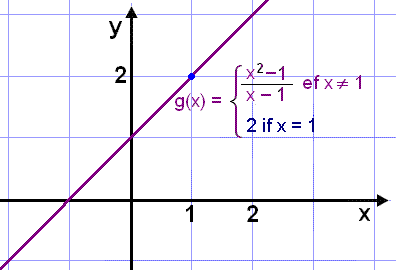 |
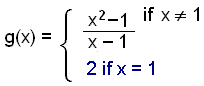
In this way we get the continuous graph shown . |
Functions that are defined in this way with more than one expression, depending on the values that x takes, are referred to as interval defined functions.
Find the value of ![]()
In this case there is no problem of dividing by zero so we can put the number 2 into the expression instead of x.
23 – 22 = 8 – 4 = 4
The function f(x) = x3 – x2 gets nearer and nearer to 4 as x gets nearer and nearer to 2.
Find
the limit
![]()
In this case we cannot give x the value 3 as that would mean dividing by zero. We can however factorise the expression in the numerator and cancel out the factor x – 3
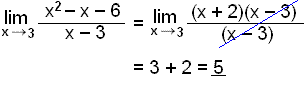 |
Put the value 3 in for x. |
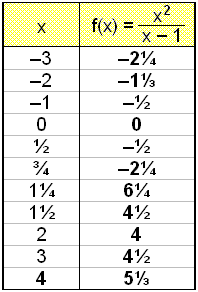
Find the limit ![]()
Now we cannot simplify the expression so we try to find a solution by putting in values of x near to 1. We choose values both slightly greater and slightly less than 1.
![]()
See the following table of values.
 |
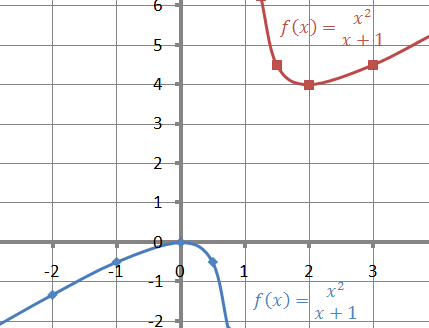 |
The graph is in two parts with a vertical asymptote in x = 1.
Let's consider what happens
as x gets near to the value 1. We can see from the graph that we have to
consider separately values above and below x = 1. We can accomplish this
easily using
EXCEL. We put numbers slightly less than 1 in column A and slightly greater than
1 in column D.
The formula in B3 will be =A3^2/(A3–1) as A3 contains has the value of x.
A corresponding formula is in E3, that is = D3^2/(D1–1). Both formula are
copied down .
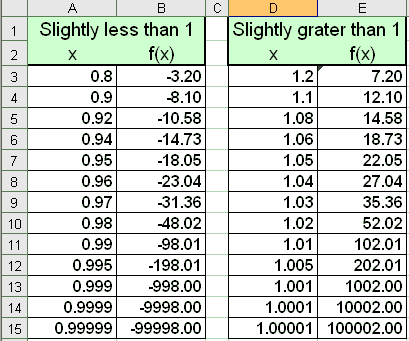
We see that when x is less than1, that is as x approaches the value 1 from the left ( the left of the number 1 on the x axis ), the values of f(x) (column B) get nearer and nearer to –∞. When x is greater than 1 that is approaches 1 from the right the function f(x) approaches +∞. Of course infinity does not exist as whatever large number you can imagine there always exists an even larger one.
We draw the following conclusion:
The limit
![]() does not exist.
does not exist.
Consider the limit ![]() .
.
We cannot put in x values
that are less than zero because the squareroot of a negative number does not
exist.
In these circumstances we can only talk about the limit from the right, that is
when x is greater than 0.
The following notation is used:
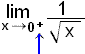
The +
sign shows that x approacches 0 from the right ( x > 0 ).
The CASIO- calculator shows the following graph:
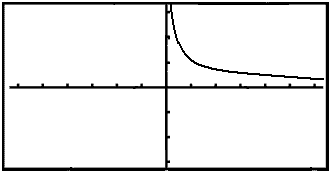
The graph comes down from
the y axis and then goes to the right along the x axis. Neither x nor f(x) take
negative values. For small values of x the y values are large
and for large x values the y values are small. It is obvious that f(x) tends to
infinity as x tends to zero, therefore 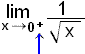 does not exist.
does not exist.
Find ![]() if it exists.
if it exists.
It is not obvious how we can cancel this expression but the fact that the value x = 1 makes both the numerator and the denominator zero tells us that factorisation is possible. Using the rule (a – b)(a + b) = a2 – b2 gives the following.
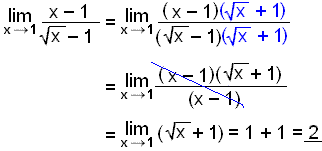
|
To find the limit of f(x) when x tends to a there are three different situations that can arise: 1. We calculate f(a) ( a is put into the expression instead of x).
2. If the numerator and the denominator of f(x) are both zero when x = a then f(x) can be factorised and simplified by cancelling. f(a) is then calculated if possible. 3. If, when x = a, the denominator is zero and the numerator is not zero then the limit does does not exist. |
|
Consider the following interval
defined function: |
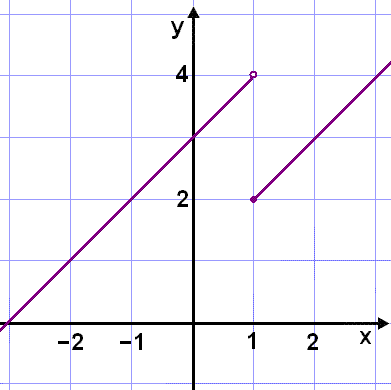 |
In this example the limit of f(x) as x tends to 1 does not exist as it depends on whether x is greater than or less than 1.
![]() and
and ![]()
|
A function f(x) is said to be continuous in the point (a, f(a)) if it exists in an interval around x = a and
If this is true for all values of x in the domain of f(x) then we say that the function is continuous. Conversely if a function is continuous then it is continuous in every point of its domain. |
We will now look at limits when x tends to + or – infinity.
This is no problem when considering polynomial functions. As x tends to infinity ( + or – ) the function also tends to infinity. Whether this is + or – infinity depends on the term with the highest power. Neither do logarithm functions, exponential functions or the square root functions present any problem.
It's a dfferent matter however with rational functions (functions in the form f(x)/g(x)).
When considering
![]() we need to look at whether it is the numerator or denominator that increases
more rapidly.
we need to look at whether it is the numerator or denominator that increases
more rapidly.
If the numerator, f(x), increases more rapidly as x tends to infinity then the limit does not exist but tends to + or – infinity.
However, if the denominator, g(x), increases more rapidly then limit is likely to tend to a specific value.
Now let's look at some examples where x tends to infinity.
a)
![]()
Here the denominator tends to infinity while the numerator
does not change. When we divide by a number that gets bigger and bigger, the
outcome gets smaller and
smaller tending to zero. So the limit is zero.
![]()
b)
![]()
Here the denominator
increases more rapidly than the numerator, so the fraction gets smaller and
smaller tending to zero.
![]()
c)
![]()
This is the reverse of b).
The numerator increases more rapidly and the outcome gets bigger and bigger
tending to infinity. We say the limit does not exist.
( NB.In some texts the limit is said to be infinity).
d)
![]()
In this example the
denominator is of a higher power than the numerator and therefore increases more
rapidly. The fraction tends to zero so
![]()
|
Is 0 if g(x)
increases more rapidly than f(x) |
Find ![]() .
.
What happens when the numerator and denominator are both polynomials of the same degree? Both increase equally rapidly. If we we divide all through by the highest power of x (in this case x2) we can find the solution.
![]()
As x tends to infinity, two terms in the numerator, x/x2 and 2/x2 tend to zero leaving us with 1 in the numerator and 2 in the denominator. The result is therefore:
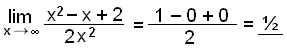
|
Problems with limits of rational functions where the numerator and denominator are polynomials of the same degree can be solved by dividing all through by the highest power of x. |
Practise these methods then take test 1 on limits.
ps. remember to fill in your check list.