© 2008  Rasmus ehf and Jσhann Νsak

Vectors

  

Lesson 5

Vectors and straight lines

Example 1:

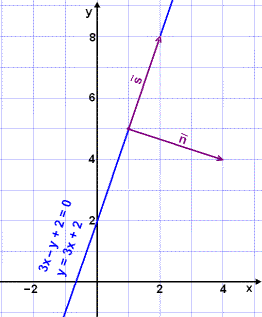
Find one vector that is parallel to the line y = 3x + 2 and a second vector that is perpendicular to the line

We begin by finding two points that lie on the line.  

    Choose x = 0 and find the corresponding y value.
    y = 3·0 + 2 = 2. The point (0, 2) lies on the line.

    Choose x = 1 and find y.

    y = 3·1 + 2 = 5. The point (1, 5) lies on the line.

Find a vector that joins these two points and can call it .
 has the same direction as the line and is called a direction vector. 

If we rotate the vector by 90Ί we get a vector that is perpendicular to the line. This is called  a Normal vector and is labelled .

The diagram shows these two vectors.

 

We can rewrite the equation of the line in the example y = 3x + 2  in the form 3x – y + 2 = 0 by moving y over the equal sign and arranging the terms so that the term in x comes first, then the term in y and finally the constant term. Note that the coefficients of x and y, 3 and –1 are the same as the coordinates of the normal vector . 

We will now show that this is true for all straight lines.

We use the general form for a straight line, ax + by + c = 0.

Find two points on the line, first by choosing  x = 0 and finding y and then by choosing y = 0 and finding x.

   a·0 + by + c = 0

                    y = –c/b if x = 0

   ax + b·0 + c = 0

                    x = –c/a if y = 0

The points (0, –c/b) and (–c/a, 0) lie on the line.

The direction vector is therefore and the normal vector is .

It‘s customary, and easier, to work with whole numbers rather than fractions so we multiply the coordinates of the vectors by ab/c. By doing this we change only the length of the vectors, not the direction. The vectors are still parallel or perpendicular to the line.

     The new direction vector will be and the new normal vector will be

To find a direction vector or a normal vector for a straight line all we have to do is write the equation in the general form. We can then read directly from the equation.

The general equation of a straight line: ax + by + c = 0.

A normal vector is

A direction vector is

We can use these vectors to find the angle between straight lines by using the scalar product of the vectors.  The angle between the lines is the same as the angle between their direction vectors. Simple geometry shows that the angle between the lines is also equal to the angle between their normal vectors.

Example 2:

Find the angle vΊ between the lines l1 , with equation y = 3x + 2 and the line l2 with equation y = x + 4 (see diagram).

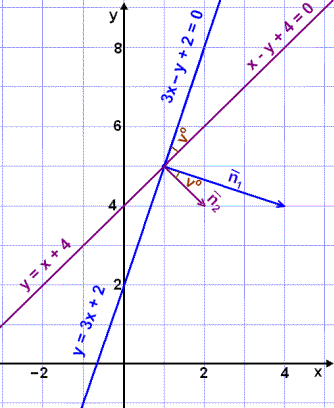
   Rearranging the equations to the general form we get: 3x – y + 2 = 0 and x – y + 2 = 0.

   The normal vectors are and

The lengths of the normal vectors are:

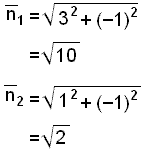
We now have all the information we need to use the scalar product to find the angle vΊ between the normal vectors, which is equal to the angle between the lines.

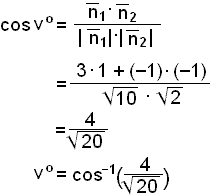
          vΊ ≈ 26.6Ί

Find a vector that starts in the point (1, 2) and is perpendicular to the vector

If we give the end point of the vector coordinates (x, y) then we can see that all vectors of the form are perpendicular to the given vector.

The scalar product of perpendicular vectors is 0 which means we can write the following equation:

   3(x – 1) + (–1)(y – 2) = 0

              3x – 3 – y + 2 = 0

                    3x – y – 1 = 0

This is the equation of a straight line which goes through the point  (1, 2) with a normal vector

This gives us a method for finding the equation of a straight line if we know one point on the line and a normal vector.

The equation of a straight line that goes through the point  (x1, y1) and has a normal vector is:

a(x - x1) + b(x - y1) = 0

 

Example 3:

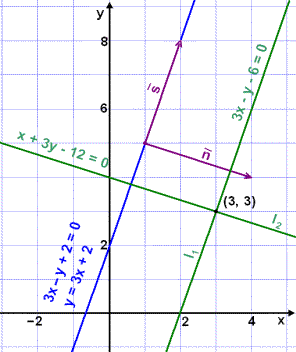
Find the equation of two straight lines l1 and l2 that intersect in the point (3, 3). l1 is parallel and l2 is perpendicular to the line 3x –y + 2 = 0 .

  The normal vector  of l1 is the same as the normal  of  3x –y + 2 = 0, that is .

  We can put this information straight into the equation

     a(x – x1) + b(x – y1) = 0

   3(x – 3) + (–1)(y – 3) = 0

              3x – 9 – y + 3 = 0

                     3x – y – 6 = 0        (equation of the line l1)

  The normal vector for l2 is the same as the direction vector of  3x –y + 2 = 0 , that is .

  Again we can put these values into the basic line equation

     a(x – x1) + b(x – y1) = 0

       1(x – 3) + 3(y – 3) = 0

              x – 3 + 3y – 9 = 0

                  x + 3y – 12 = 0         (equation of the line l2)

Finally, let‘s look at the diagram.

 

Example 4:

Find the distance between the parallel lines 3x – y + 2 = 0 and 3x – y – 6 = 0 (see the diagram).

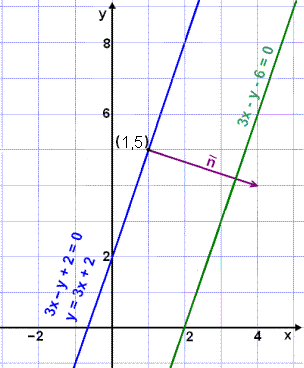
We choose any point, for example (1, 5), on the line 3x – y + 2 = 0 and find the shortest distance of the point from the other line
3x – y – 6 = 0. This will give us the required distance between the two lines.

The length of the normal vector is not usually the required distance.

From the diagram we can see that in this example the normal vector, , is longer than the distance between the two lines. We therefore need to find a number t that, when  multiplied by  the , gives us a vector that is exactly the right length.
Call the end point of the vector (on the second line) (x, y). We can now write the following vector equation:

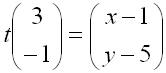
This gives us two equations that can be solved for  x and y.

   3t = x – 1          and          –t = y – 5

     x = 3t + 1                         y = –t + 5

The point ( x, y ) lies on the second line so we can put these x and y values into the equation of the line.

                      3x – y – 6 = 0

   3(3t + 1) – (–t + 5) – 6 = 0   

         9t + 3 + t  – 5 – 6 = 0  

                                10t = 8

                                   t = 0,8

In example 2 we found that the length of   was .

The distance between the two lines is therefore t· or the required distance is 0.8· 

We will now do the above example with letters instead of numbers. This leads to a very useful formula for the distance of a point from a line.

    The general equation of a straight line is ax + by + c = 0 and we choose a point with coordinates (x1, y1).
    Now we can write the following equation:

   

    We solve this vector equation for x and y.

         ta = x – x1          and          tb = y – y1

          x = ta + x1                        y = tb + y1

    Putting these values into the equation and solving for t:

                              ax + by + c = 0

         a(ta + x1) + b(tb + y1) + c = 0

           ta2 + ax1 + tb2 + by1 + c = 0

                                    ta2 + tb2 = –ax1 – by1 – c

                                   t(a2 + b2) = –ax1 – by1 – c

The length of the normal vector is given by ||2 = a2 + b2 so we can rewrite the equation as:

         t·||2 = –ax1 – by1 – c

If we divide through by ||2 we get a value for t, which we can multiply by the length of the normal vector . We need to remember that length cannot be negative so we use the absolute value sign.

       t = |–ax1 – by1 – c| /||2

If we multiply by || we get the following formula:
 

The distance of the point (x1, y1) from the line ax + by + c = 0 is

or

 

Example 5:

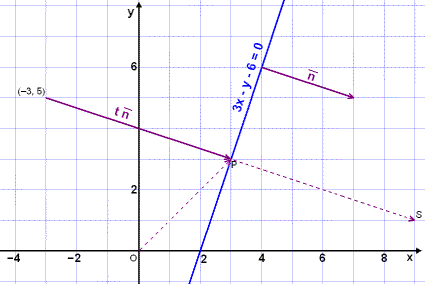
We are now going to reflect the point (–3, 5) in the line 3x – y – 6 = 0 and find the point of reflection.

The plan is as follows. First find a vector that is perpendicular to the line 3x – y – 6 = 0 going from the point (–3, 5) to the point
P = (x, y), which lies on the line. This will be the normal vector t  (see the diagram). We find the reflected point S by adding the vector t  to the position vector of P.

We begin by finding the value of t with the same method as in the previous example:

   

  

Solving these two equations for x and y we get:

   3t = x + 3        and        –t = y – 5

    x = 3t – 3                      y = –t + 5

Putting these values for x and y into the equation we can find t.

                      3x – y – 6 = 0

   3(3t – 3) – (–t + 5) – 6 = 0

            9t – 9 + t – 5 – 6 = 0

                                 10t = 20

                                     t = 2

This gives us the vector and we can find the coordinates of the position vector of P.

Now we add 2  ( t) to this and get the position vector for S.

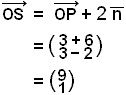
The coordinates of the point of reflection: S = (9, 1)

Example 6:

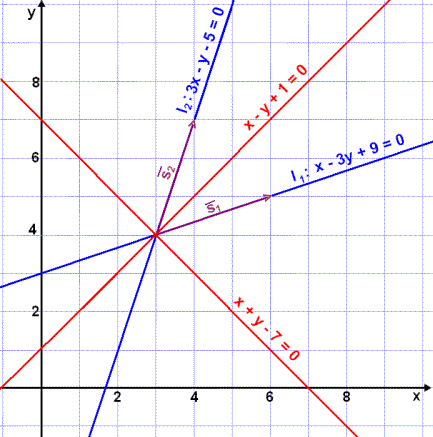
Find the equations of two lines l1 and l2 that intersect in the point (3, 4) and are parallel to the vectors and respectively.

Then find the equation of the angle bisector of the angle between the two lines.

The normal vectors of l1 and l2 are and

The equation of  l1 is therefore:

   1(x – 3) – 3(y – 4) = 0

        x – 3 – 3y + 12 = 0

             x – 3y + 9 = 0

and the equation of l2 is

   3(x – 3) – 1(y – 4) = 0

          3x – 9 – y + 4 = 0 

              3x – y – 5 = 0.

All points (x, y) on the angle bisector are equidistant from the lines  l1 and l2. We can therefore find the equation of the angle bisector by finding the distance of (x, y) from each line and equating them.

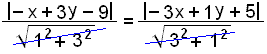
        –x + 3y – 9 = ±(–3x + y + 5)

± because of the absolute value

This gives us two equations.

   –x + 3x + 3y – y – 9 – 5 = 0    or    –x – 3x + 3y + y – 9 + 5 = 0

                     2x + 2y – 14 = 0                              –4x + 4y – 4 = 0

                           x + y – 7 = 0                                    x – y + 1 = 0

There are two answers because there are two angles between the lines and therefore two angle bisectors (see diagram).


 

Try Quiz 5 on Vectors.
 Remember to use the checklist to keep track of your work.