© 2008  Rasmus ehf  and Jóhann Ísak

Triangles

Lesson 2   Some important characteristics

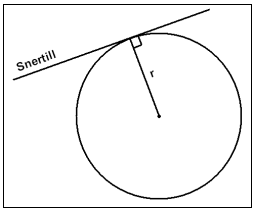
A straight line that intersects a circle only once (touches the circle) is called a tangent to the circle. The angle between the radius and a tangent  at the point of intersection is always 90°.

A straight line that divides an angle into two equal parts is called the angle bisector. All points on the angle bisector are equidistant from the arms or sides of the angle which is bisected. A circle, drawn such that the sides of an angle are tangents to the circle, has it’s centre on the angle bisector.

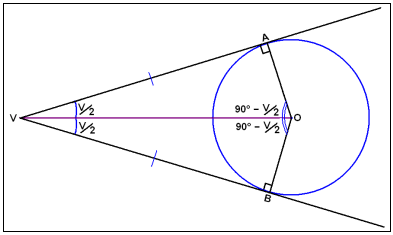
On the diagram above the line from V through O is the angle bisector of angle V. The line segments VA and VB are of equal length and are perpendicular to AO and BO respectively. 

In the diagram below the angle V = 40° and the line segments VA and VB  are 40 cm. Find the angle AOB, labelled x,  and the radius of the circle.

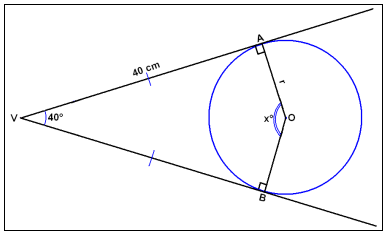
VAOB is a quadrilateral and therefore the sum of the angles is 360° . We know three of the angles and can therefore calculate the fourth.

   x° = 360° − 90° − 40° − 90° = 140°

     tan 20° = ^x/₄₀

                 x = 40×tan 20° ≈ 14,6 cm

An angle bisector  divides the side of the triangle opposite to the angle in the same ratio as the line segments that are adjacent to the angle.

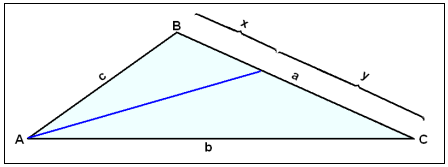
The angle bisector of angle A divides the side a in the ratio c/b. If we call these parts x and y then the following rule holds:

Triangle ABC has the following measurements:

   a = 30 cm, b = 40 cm og c = 20 cm.

The angle bisector of angle A divides the side a into two parts. Calculate the length of these parts.  We use the same notation as in the rule above.

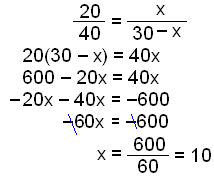
The side a is divided into parts of length 10 cm and 30 − 10 = 20 cm.

Every triangle has one point that is equidistant from all three sides of the triangle. This is the point in which the angle bisectors of all the angles of the triangle intersect. Using this point as the centre we can draw a circle that touches all three sides of the triangle. This is called the inscribed circle of the triangle.

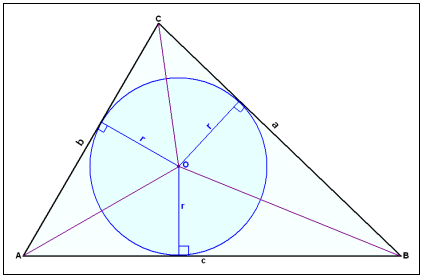
We can see from the diagram above that the angle bisectors AO, BO and CO divide the triangle into three smaller triangles each of which has the height r. Their areas are ½×a×r, ½×b×r and ½×c×r.  The total area, that is the area of the triangle ABC, is therefore:

  Area  F = ½×a×r + ½×b×r + ½×c×r = ½×r(a + b + c)

The circumference of the circle, lets call it u, is a + b + c  which means that we can write the formula for the area of a triangle as:

There is a second point, that can be either inside or outside the triangle, that is equidistant from all the angles of the triangle. This point is where all three perpendicular bisectors of the triangle intersect. This is because points on the perpendicular bisector are equidistant from angles  that form the end points of the sides that they bisect.

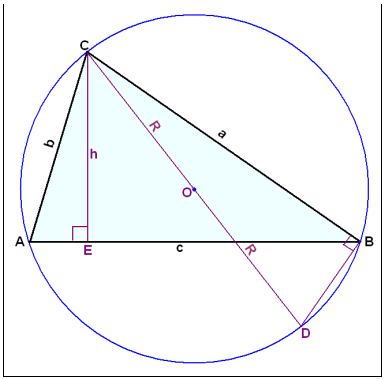
The above diagram shows the triangle ABC with it’s circumscribed circle. Two right angled triangles have been drawn In the diagram. Triangle ACE is formed by drawing the height h from angle C to the side c. Triangle  BCD is found by drawing the diameter of the circle from C through the centre O to a point D on the circle. Triangles ACE and BCD are similar as they are both right angled triangles and angle A = angle D . (both span the arc CB) Therefore the following ratios hold:

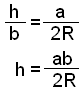
Putting this value for h into the formula for the area F  of a triangle, F = ½×c×h  we get the following result:

We can also use the following:

Which leads to the rule:

If we solve for h and put the value h = b×sin A into the formula for area  F = ½×c×h  we obtain the rule for the area of a triangle:

Example 3

A triangle has sides of length 17 cm, 17 cm and 16 cm.

a) Find the area of the triangle.

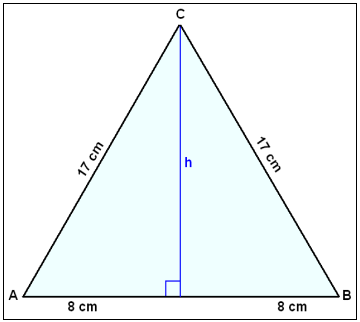
Use Pythagoras’ rule to find the height h.

  h² + 8² = 17²

           h² = 289 − 64 = 225

            h = 15 cm

Now we can calculate the area F.

   F = ½×16×15 = 120 cm² 

b) Find the radius of the inscribed circle.

The perimeter of the triangle  u = 17 + 17 + 16 = 50 cm.

Area F = 120 = ½×r×50

           r =120×2/50 = 14.8 cm

c) Find the radius of the circumscribed circle.

    Area F = 120 = 17×17×16/4R

        480R = 17×17×16

            R = ^17×17×16/₄₈₀ = ²⁸⁹/₃₀ ≈ 9,6 cm

d) Find the angles of the triangle.

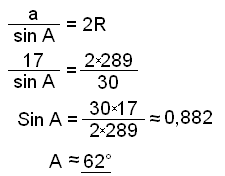
Therefore B ≈ 62° and C ≈ 180 − 2×62 ≈ 56°.

A median in a triangle is a line segment drawn from an angle to the midpoint of the opposite side. The medians of a triangle all intersect in one point. This point divides each median in the ratio 1: 2.

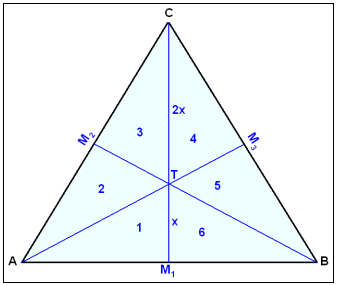
In the above diagram M₁, M₂ and M₃ are the mid points of the sides of the triangle. The medians intersect in the point T which divides M₁C into the parts x and 2x.

The medians divide the triangle into six smaller triangles, numbered 1-6 in the diagram. These triangles all have the same area. The point T is therefore the centre of gravity of the triangle. If the triangle was made of material and cut out then we would be able to balance it on a pin or nail placed at the point T.

circumscribed circles are in the same point.

The medians of a triangle intersect in one point.

Example 4

The length of the median of a triangle is 24 cm. Calculate the length of the line segments that the other medians divide it into.

We call one segment x, the other is then 2x.

    x + 2x = 24

          3x = 24

            x = 8

Example 5

A triangle ABC is drawn in a coordinate system.
A = (−4, −4), B = (12, 0) and C = (4, 16). Find the coordinates of the point where the medians intersect.

We begin by finding the mid point of side BC

Now we find the equation of the median through A. This is the line through  A = (−4, −4) and (8, 8).

   The gradient k = (8 + 4)/(8 + 4) = 1

Using the equation of a straight line in the form:

   y = k(x − x₁) + y₁

  we get  y = 1(x − 8) + 8

   y = x

Next we do the same for the median through the point B. First we find the midpoint of AC.

The equation of the median through B is now found. This is the line through  B= (12, 0) and (0, 6).

The gradient   k = (0 − 6)/(12 − 0) = −½

 Therefore  y = −½(x − 0) + 6

   y = −½x + 6

Solving the two equations y = x and y = −½x + 6 we get:

   x = −½x + 6

   x + ½x = 6

       1½x = 6

            x = 4 and therefore y = 4 also.

Ceva’s Rule:

This is a rule that is named after the Italian mathematician Giovanni Ceva,

If we draw any three lines in a triangle that all go through  one point, say P and an angle of the triangle. Call the points where  they cut the sides AB, AC and BC , X, Y and Z  respectively.

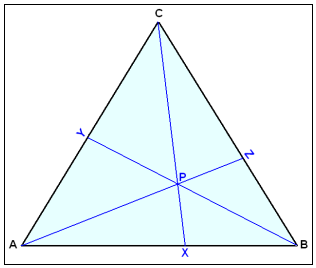
Then the rule is as follows:

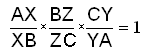
This rule holds of course for medians, heights and any other lines that go from one angle of a triangle to the opposite side and intersect in one point.

In the diagram below find the length of the line segments that Z divides BC into.

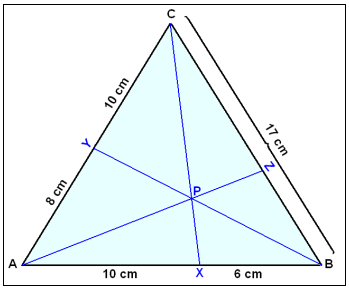
If x = BZ, then ZC = 17 − x. Using the rule we get:

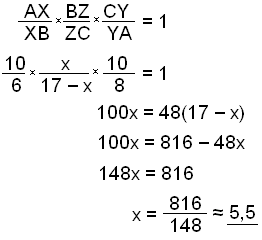
Therfore Z divides the side BC into segments of length 5.5 cm and 11.5 cm.

Try Quiz 2 on Triangles.  Remember to use the checklist to keep track of your work.