| © 2008 Rasmus ehf and Jóhann Ísak Pétursson | Equations III |
|
Lesson 2 Cubic and quartic equations
x3 − x2 – 4x + 4 = 0
There is an extremely complicated formula for solving cubic equations. Some calculators have this formula built in and therefore can be used to solve cubic equations.
We are going to learn how these equations can be solved by factorising. If the equation has solutions that are integers a, b and c then we can factorise the equation as follows:
x3 − x2 – 4x + 4 = (x − a)(x − b)(x − c) = 0
Multiplying the brackets together we see that the constant term, 4, must be the number we get when we multiply a, b and c together.
abc = 4
All the solutions a, b and c must be factors of 4 so there are not many whole numbers that we need to consider.
We have only the following possibilities:
±1, ±2 and ±4
We’ll examine each of these numbers to find which ones are solutions of the equation.
f(1) = 13 − 12 – 4×1 + 4 = 0 1 is a solution
f(−1) = (−1)3 − (−1)2 – 4×(−1) + 4 = 6
f(2) = 23 − 22 – 4×2 + 4 = 0 2 is a solution
f(−2) = (−2)3 − (−2)2 – 4×(−2) + 4 = 0 −2 is a solution
We have now found three solutions so we don’t need to try 4 and −4 as a cubic equation has a maximum of three solutions.
These three numbers give us the values of a, b and c and we can factorise the equation.
x3 − x2 – 4x + 4 = (x − 1)(x − 2)(x + 2) = 0
This method involves finding integers that are factors of
( can be divided into ) the constant term and then testing whether these
integers are solutions of the equation.
Unfortunately we cannot assume that the solutions of a third degree equation are
all integers.
However, if we can find one integer solution, lets say it is x = a then, by the
remainder theorem , we know that (x − a) is a factor of the equation. We
can find another factor, a quadratic factor, by division. We can then solve the quadratic equation by using the
formula for solving quadratics.
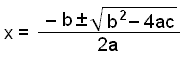
Example 1
Solve the equation x3 − 3x2 – 2x + 4 = 0
We put the numbers that are factors of 4 into the equation to see if any of them are correct.
f(1) = 13 − 3×12 – 2×1 + 4 = 0 1 is a solution
f(−1) = (−1)3 − 3×(−1)2 – 2×(−1) + 4 = 2
f(2) = 23 − 3×22 – 2×2 + 4 = −4
f(−2) = (−2)3 − 3×(−2)2 – 2×(−2) + 4 = −12
f(4) = 43 − 3×42 – 2×4 + 4 = 12
f(−4) = (−4)3 − 3×(−4)2 – 2×(−4) + 4 = −100
The only integer solution is x = 1. When we have found one solution we don’t really need to test any other numbers because we can now solve the equation by dividing by (x − 1) and trying to solve the quadratic we get from the division.
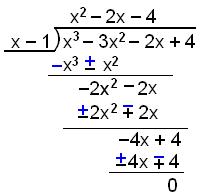
Now we can factorise our expression as follows:
x3 − 3x2 – 2x + 4 = (x − 1)(x2 − 2x − 4) = 0
It now remains for us to solve the quadratic equation.
x2 − 2x − 4 = 0
We use the formula for quadratics with a = 1, b = −2 and c = −4.
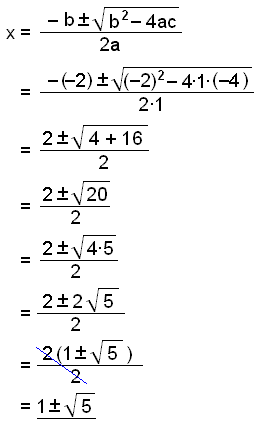
We have now found all three solutions of the equation x3 − 3x2 – 2x + 4 = 0. They are: eftirfarandi:
x = 1
x = 1 + Ö5
x = 1 − Ö5
Example 2
We can easily use the same method to solve a fourth degree equation or equations of a still higher degree. Solve the equation f(x) = x4 − x3 − 5x2 + 3x + 2 = 0.
First we find the integer factors of the constant term, 2. The integer factors of 2 are ±1 and ±2.
f(1) = 14 − 13 − 5×12 + 3×1 + 2 = 0 1 is a solution
f(−1) = (−1)4 − (−1)3 − 5×(−1)2 + 3×(−1) + 2 = −4
f(2) = 24 − 23 − 5×22 + 3×2 + 2 = −4
f(−2) = (−2)4 − (−2)3 − 5×(−2)2 + 3×(−2) + 2 = 0 we have found a second solution.
The two solutions we have found 1 and −2 mean that we can divide by x −
1 and x + 2 and there will be no remainder. We’ll do this in two steps.
First divide by x + 2
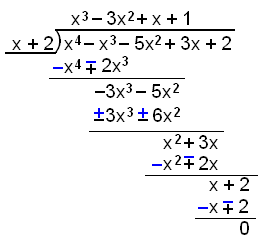
Now divide the resulting cubic factor by x − 1.
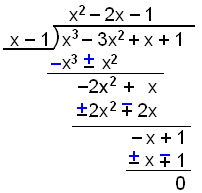
We have now factorised
f(x) = x4 − x3 − 5x2 + 3x + 2 into
f(x) = (x + 2)(x − 1)(x2 − 2x − 1) and it only
remains to solve the quadratic equation
x2 − 2x − 1 = 0. We use the formula with a = 1, b = −2 and c = −1.
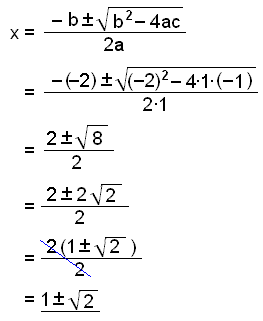
Now we have found a total of four solutions. They are:
x = 1
x = −2
x = 1 + ![]()
x = 1 − ![]()
Sometimes we can solve a third degree equation by bracketing the terms two by two and finding a factor that they have in common. Lets look at an example of this.
Example 3.
Solve the equation x3 − 2x2 − 4x + 8 = 0
x3 − 2x2 − 4x + 8 = 0 (x3 − 2x2) − (4x − 8) = 0 [x2(x − 2) − 4(x − 2)] = 0 (x − 2)[x2 − 4] = 0 (x − 2)(x − 2)(x + 2) = 0 |
Here the bracket (x − 2) is a common factor and can be taken outside a common bracket. |
Notice that the bracket (x − 2) occurs twice when we have finished factorising. x = 2 is therefore a double solution and we have only two different.They are:
x = 2 and x = −2.Lausnir: x = 2 og x = −2.
The examples we have looked at so far are all equations where the term with the highest power has the coefficient 1.
How do we deal with equations where this coefficient is some other number?
The general form is f(x) = ax3 + bx2 + cx + d where a, b, c, and d are integers.
We can look for integer solutions in the same way as before by testing the factors of the constant term d. If we find an integer solution then we can divide and find the other solutions as before.
If none of the factors of d give us a solution
then we look for solutions that are fractions.
Let’s assume there is a solution that is a fraction and let’s call this
solution x = t/n.
This means that x − t/n is a factor of f(x), or, if we multiply through by n then xn − t is a factor.
Now let’s assume we have divided f(x) by xn
− t and have found the quadratic factor, we can call it
Ax2 + Bx + C.
We now have the result that
ax3 + bx2 + cx + d = (xn − t )( Ax2 + Bx + C )
comparing the coefficients of x3 on
both sides of the equation we see that a = nA and therefore n must be a factor
of a.
Similarly, comparing the constant terms, we see that
d = −tC and therefore t is a factor of d.
We conclude any fraction that is a solution of the cubic equation ax3 + bx2 + cx + d must be of the form t/n where t is a factor of the number d and n is a factor of the number a.
Generalising for a function of degree n:
f(x) = anxn + an−1xn−1+ × × × × + a1x + a0
with coefficients a0, a1, a2, × × × × × an−2, an−1 and an .
If this function has a rational solution, say t/n, then t is a factor of a0 and n is a factor of an .
Example 4
Solve the equation f(x) = 2x3 − 7x2 + 4x + 3 = 0.
The possible integer roots of f(x) are the factors of 3, they are ±1 and ±3. The fractions that can be roots are these four numbers divided by the factors of 2. So the complete list of rational numbers that we need to consider is ±½, ±1, ±3/2 and ±3.We can see at once that we don’t need to consider any negative values as they will all give negative values for f(x), not 0.
Now let’s try the other possibilitiesf(½) = 2(½)3 − 7(½)2 + 4×½ + 3 = 3½
f(1) = 2×13 − 7×½2 + 4×1 + 3 = 2
f(3/2) = 2(3/2)3 − 7(3/2)2 + 4×3/2 + 3 = 0 so we have found a solution.
x = 3/2 is a solution so (x − 3/2) is a factor. Dividing by (x − 3/2) can be difficult. So we multiply through by 2 and divide by (2x − 3) instead. If (x − 3/2) is a factor
then so is (2x − 3) .
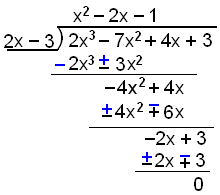
We now have to solve the equation x2 − 2x − 1 = 0. We have already solved this equation in example 2.
The solutions were 1 + ![]() 2 og 1 −
2 og 1 − ![]() 2.
2.
So we have found three solutions. They are:
x = 3/2 = 1½
x = 1 + ![]() 2
2
x = 1 − ![]() 2
2
Try Quiz 2 on Equations III.
Remember to use the checklist to keep track of your work.