© 2008 Rasmus ehf and Jóhann Ísak Pétursson
© 2008 Rasmus ehf and Jóhann Ísak Pétursson |
Equations III |
|
Lesson 1
Quadratic equations
We are now going to look at how to solve quadratic equations (second degree equations). This is the same process as finding where the graph of a quadratic function such as
f(x) = ax2 + bx + c crosses the x-axis
First we will consider equations where the coefficients b or c are zero (b = 0 or c = 0).
Example 1
| a) 2x2 − 8 = 0 2x2 = 8 x2 = 4 x = ±2 |
First move the constant term over the equals sign, next divide both sides of the equation by 2. Finally take the square root of both sides of the equation remembering the + and −. |
| b) 2x2 + 8 = 0 2x2 = −8 x2 = −4 no solution |
In this example we can’t take the square root because of the minus sign. |
Example 2
| a) 2x2 − 8x = 0 2x(x − 4) = 0 2x = 0 eđa x − 4 = 0 x = 0 eđa x = 4 |
Factorise by taking 2x outside a bracket. One of the two factors must be zero in order for the multiplication to be zero. |
| b) 2x2 + 8x = 0 2x(x + 4) = 0 2x = 0 eđa x + 4 = 0 x = 0 eđa x = −4 |
Again we have two solutions. Quadratic equations where c=0 always hve two solutions. |
We
have a more difficult problem if none of the coefficients
a, b and c are zero.
The easiest type to solve are equations that fit into the pattern
p2 ± 2pq + p2 = (p ± q)2
Example 3
| a) x2 + 2x + 1 = 0 (x + 1)2 = 0 (x + 1) = 0 x = −1 |
This fits exactly into the above pattern. |
| b) 2x2 − 8x + 8 = 0 2(x2 −4x + 4) = 0 2(x – 2)2 = 0 (x − 2) = 0 x = 2 |
If we take 2 outside a bracket this too fits the pattern. |
Sometimes we can factorise the equation by inspection (guessing the factors), then finding the value of x that makes each factor zero.
Example 4
Solve the equation x2 − 5x + 6 = 0
x2 − 5x + 6 = 0
(x − 2)(x − 3) = 0
x = 2 or x = 3
Example 5
| Solve the equation x2 − 4x − 5 = 0.
x2 − 4x − 5 = 0 x2 − 4x + 22 − 22 − 5 = 0 (x2 − 4x + 4) − 9 = 0 |
Here we complete the square by adding in ( and then subtracting) half the coefficient of b squared. We can then use the rule p2± 2pq + q2 = (p ± q)2 |
| (x − 2)2 − 9 = 0 |
The result is in the form (x + r)2 + s |
x − 2 = ±3 x = 2 ± 3 x = 5 or x = −1 |
which was introduced in the 3rd. lesson of Functions 1 |
Example 6
Solve the equation 3x2 − 24x + 21 = 0
3(x2 − 8x) + 21 = 0
3(x2 − 8x + 42) − 3∙42 + 21 = 0
3(x − 4)2 − 48 + 21 = 0
3(x − 4)2 = 27
(x − 4)2 = 9
x − 4 = ±3
x = 4 + 3 = 7 or x = 4 − 3 = 1
Example 7
We are now going to find a formula which we can use to solve any second degree equation of the form ax2 + bx + c = 0
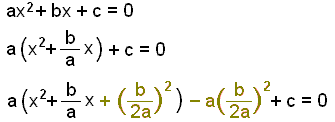 |
Take a outside a bracket.. Add half the coefficient of x squared. Subract the same number remembering to multiply by a. |
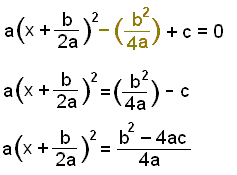 |
Write the first three terms of the equation as a bracket squared Move the other two terms over the equals sign and find the common denominator. |
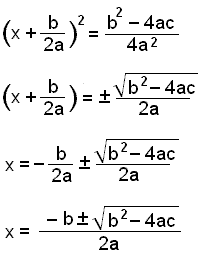 |
Now take the square root of both sides of the equation remembering the + and −. Finally solve for x by moving the term inside the bracket over the equal sign. |
The algebra in this proof is quite complicated but once we have found the formula we don’t have to go through the process again and we can use it to solve any quadratic equation.
This is the formula we can use to solve the equation ax2 + bx + c = 0
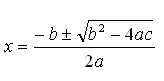 |
This formula is one of the best known and most useful formulas in mathematics.
Example 8
We will now use this formula to solve the equation 2x2 − 10x + 8 = 0
| The coefficients are: | a = 2 |
| b = −10 | |
| c = 8 |
Put these numbers for a,b and c into the formula
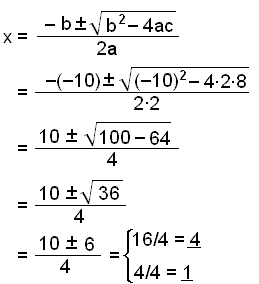
Example 9
Solve the equation x2 − 3x + 6 = 0
The coefficients are a = 1, b = −3 and c = 6.
Putting them into the formula.
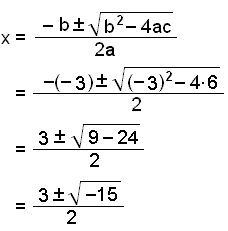
In this example the number under the square root is negative so the equation has no solution.
| Example10 |  |
We can solve quadratic equatons using a graphical calculator.
This is how to solve the equation 2x2 − 10x + 8 = 0 using a graphical calculator.
First choose „EQUA“ on the menu.
We then get :
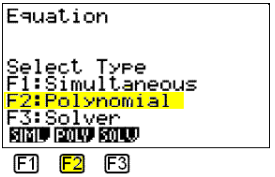
Now choose „Polynomial“ with F2 .

We solve the quadratic equation by choosing 2 (press F1). We can also solve third degree equations by choosing 3. This is the screen that we see:
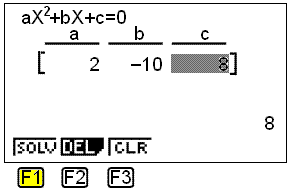
We put in the values a = 2, b = −10 and c = 8 pressing exe between each value.
The following shows the sequence of actions:
![]()
Finall choose SOLV by pressing F1. The solutions 4 and 1 appear on the following screen:
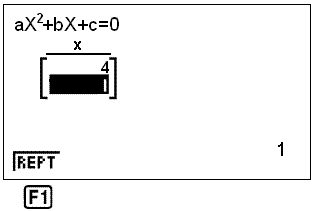
Example 11
Let’s see how the calculator deals with an equation that has no solution. Look at the equation x2 − 3x + 6 = 0. we enter the values a = 1, b = −3 and c = 6. The calculator gives the following solution:
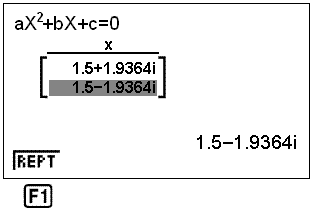
This means that the answer is what is known as a Complex number not a Real number. No Real number solution exists.
Example 12
We will now see
how we can use EXCEL to solve a quadratic equation.
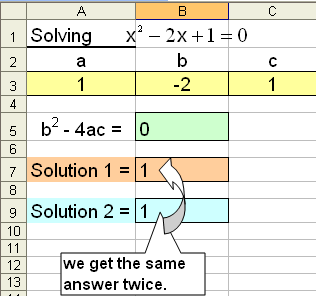
We are going to use EXCEL to solve the equation 2x2 − 10x + 8 = 0.
Write a, b and c in cells A3, B3 and C3.
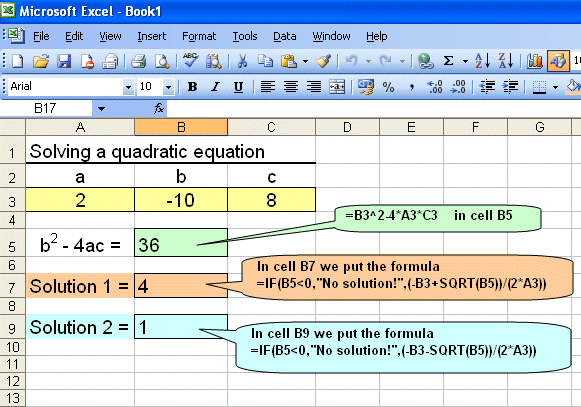
We write the formula
=B3^2-4*A3*C3 in cell B5
In cell B7 we put the formula
=IF(B5<0,"No solution!",(-B3+SQRT(B5))/(2*A3))
In cell B9 we put the formula
=IF(B5<0,"No solution!",(-B3-SQRT(B5))/(2*A3))
If we use this program to solve an equation that has only one solution, for example x2 − 2x + 1 = 0, we get the same answer twice.
If the equation has no solution, such as the equation
x2 − 3x + 6 = 0 then this is what EXCEL will give us:

Try Quiz 1 on Equations III.
Remember to use the checklist to keep track of your work.