© 2007  Rasmus ehf    og Jóhann Ísak

Sets I

Print

Lesson 3

The Real numbers

We can think of  the number line ( x – axis ) as a continuous row of points. Each point on the line denotes the distance of that point from the origin. We use  a negative sign (−)  if the point is to the left of the origin and a positive sign (+) if the point is to the right of the origin.

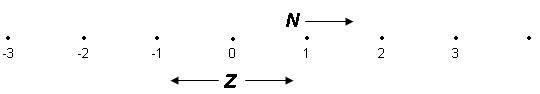
The set  of rational numbers Q can also be found on the line but again there are still other numbers. There are infinitely many numbers in between the ones we have already mentioned that cannot be written as fractions and therefore are not in the sets we have dealt with.

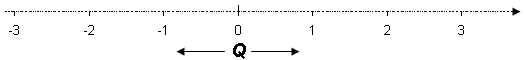
The missing numbers are called irrational numbers. They are numbers that have an infinite number of digits after the decimal point but the digits don’t repeat themselves in any pattern and are therefore not periodic. Here are a few examples:

    0.909009000900009

    0.123456789101112

    Ö2 = 1.41421356237

    Ö3 = 1.73205080756

    p = 3.141592653589

The irrational numbers together with  Q (which contains the sets  Z and N) form the continuous line of numbers that we know as the real number line ( the x- axis ). Together these sets form the set of Real numbers symbolised by the letter R.

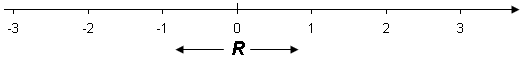
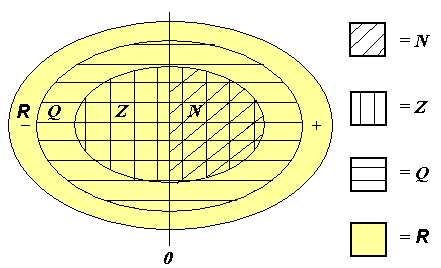
The following diagram shows the relation between the sets R, Q, Z and N. The set R contains the other sets and can be divided into rational numbers and irrational numbers. The part of the diagram that is not marked by lines contains the irrational numbers. The part marked by horizontal lines shows the rational numbers. (the set Q). The set Q divides into whole numbers ( the set Z) and fractions that are not whole numbers. Finally Z divides into whole positive numbers (the set N ) and negative numbers with zero.

We can describe intervals on the real number line in various ways. For example the interval between 1 and 5 including both these numbers can be written as follows:

Using an inequality:                 1 £ x £ 5

Using Set notation:   { xÎR | 1 £ x £ 5}

With a diagram:

Another way is by introducing a new set of symbols called interval brackets. The above example can be written:

An interval such as [1; 5] where both the end points are included is called a closed interval.

If we want to write an expression for an interval between two numbers, that is not including the end points, we use a slightly different notation.

For example the numbers that are less than 5 but greater than 1.

Using an inequality:             1 < x < 5

Using Set notation:     { xÎR | 1 < x < 5}

With a diagram:          

Interval brackets:     á1; 5ñ or ]1, 5[  (depending on the text book used)

Notice that the diagram has open circles or holes at the ends to show that we don’t include the numbers 1 and 5.

 Notice also that we use a different type of bracket to show that the end points are not included. Intervals like á1, 5ñ  where neither endpoint is included are called open intervals.

Finally we’ll look at intervals where only one end point needs to be used.

For example, if x is greater than or equal to 1 we can write:

An inequality:             x ≥ 1

Using Set notation:     { xÎR | x ≥ 1}

Diagram:

Interval notation:       [1; ®ñ  or  [1, ∞[  (again it varies in text books)

This type of interval is said to be half open (or half closed). Half open intervals don’t always stretch to infinity. For example the interval [1, 5ñ, where 1 is included but 5 is not, is half open. The diagram showing this interval is below.

Try Quiz 3 on Equations Sets I.  
Remember to use the checklist to keep track of your work.