© 2009 Rasmus ehf    & Jσhann Νsak

Functions 2

Lesson 6

Inverse functions

We have already seen some functions that are the inverse of each other.  The functions  f(x) = x2 and g(x) = √x  are the inverse of each other if we limit the x values to
non - negative numbers. These functions cancel each other out in the sense that if we apply first one function and then the other to a number then it's as if nothing has happened, the number is the same as it was to begin with. Look at the following example:

   f(x) = x2 and g(x) =

   f(2) = 22 = 4 and g(4) = √4 = 2

   f(g(a)) = = a

   g(f(a)) =  = a

It doesn't matter which of the two functions f(x) or g(x)  we apply first, the result is the same. The range of one fuction becomes the domain of the other.

A function has an inverse only if it is one - to - one and onto. In this case we limit our values of x to non negative numbers so that the function f(x) = x2 satisfies this condition. In other words a function has an inverse if it is increasing or decreasing on it's domain.  The function  g(x) = √x is increasing and can only take non - negative numbers  which again means that f(x) = x2 is limited to non - negative numbers.

We can find the equation of an inverse function algebraically by solving the equation of the function for x. Look at the following example:

 

Example 1

Find the inverse of the following functions:

a)   f(x) = 2x + 4

          y = 2x + 4                put y instead of f(x)

      –2x = 4 – y

          x = –2 + ½y              We have divided through by  –2

      This is an equation where x is a function of y. The name of the variable doesn't matter so we can exchange the x and the y . If we call this function g we get the equation of the inverse function of f(x).

g(x) = y = ½x – 2.

       We can check our result by putting in a number.

          f(1) = 2·1 + 4 = 6 and g(6) = ½·6 – 2 = 3 – 2 = 1

      If we use the general value  a, we get

         f(a) = 2a + 4  and  g(2a+4) = ½·(2a+4) – 2 = a + 2 – 2 = a

b)   f(x) = sin 2x,  Df = [–/4,/4ρ , f(x) is increasing on this interval and therefore has an inverse function.

          y = sin 2x

        2x = sin–1 y

          x = ½ sin–1 y

      The inverse function is g(x) = ½ sin–1 x.

   In most books the inverse of a function is written using the index  –1 so that f(x) has the inverse function f –1(x). This does not mean 1/f, it's simply a notation for the inverse function.  

      In the above example f –1(x) = ½ sin–1 x.

      Check.

         f(/12) = sin 2/12 = ½ 

         f –1(½) = ½·sin–1 ½ = ½·/6 = /12

c)   f(x) = e2x

          y = e2x

      ln y = ln e2x = 2x

          x = ½ ln y

      The inverse  function of  f(x) is therefore  f –1(x) = ½ ln x.

d)   f(x) = x2 – 1, Df = R+

          y = x2 – 1

          x2 = y + 1

           

The inverse function is 

       

   e) 

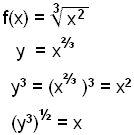We choose Df = R+ and cube both sides of the equation

Then take the square root

        The inverse function is  

 

If the function f(x) is either always increasing or always decreasing then it has an inverse function f –1(x).

The Range of f(x) becomes the Domain of f –1(x).

We find the equation of the inverse by solving the equation   y = f(x) for x.

 

Example 2

How do we need to limit the domain of the function  f(x) = sin x so that it has an inverse function? We know that a continuous function that is always increasing ( or decreasing ) has an inverse.

So we look at the derivative of the function f(x) = sin x , f΄(x) = cos x.  

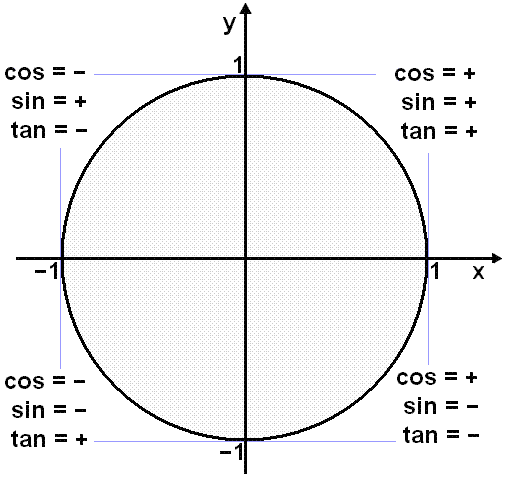
Using the unit circle we can see that  cos x is positive from  –/2 to  /2 and negative on the rest of the circle.

Look at the graph of f(x) = sin x.

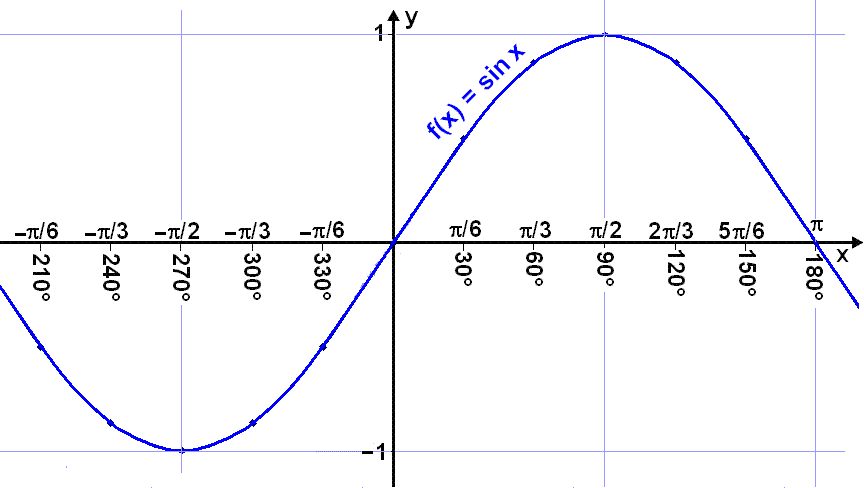
       We see that the graph is increasing on  –/2 < x < /2  so  f(x) = sin x has an inverse if we limit the domain to this interval.
 We could have chosen another interval, for example  /2 < x < 3/2 where the function is  decreasing but commonly the interval –/2 < x < /2  is chosen.

Example 3

Find the interval on which the function  f(x) = x2 – 4x + 3 is increasing, limit the domain to this interval and then find the formula for the inverse function.  Finally draw the graph of both f(x) and f–1(x)  in the same coordinate system.

We begin by finding the vertex of the parabola by differentiating and finding where the derivative is zero. ( The tangent to f(x) at the vertex is horizontal and therefore the derivative is zero )

   f(x) = x2 – 4x + 3

   f΄(x) = 2x – 4 = 0

      2x = 4

        x = 2

The vertex is where  x = 2 and the function is increasing after that. We therefore choose the domain  

Df = .

To find the equation of the inverse we need to solve the equation  y = x2 – 4x + 3 for  x.

               y = x2 – 4x + 3

         y – 3 = x2 – 4x

   y – 3 + 4 = x2 – 4x + 4

         y + 1 = (x – 2)2


Complete the square by adding half the coefficient of x (2 ) squared (4) to both sides of the equation and using the rule  
a2 – 2ab + b2 = (a – b)2.

 

We choose the + as x is on the interval 

Put in an x instead of the y

 

Now we draw the graph by first making a table of values.

Calculating f(2) tells us that f(x) = y takes values from  –1 upwards ( the function is increasing ). We need therefore to start by finding  f–1(–1).

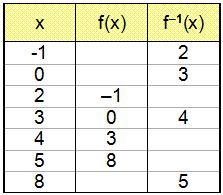
The two graphs are shown below.

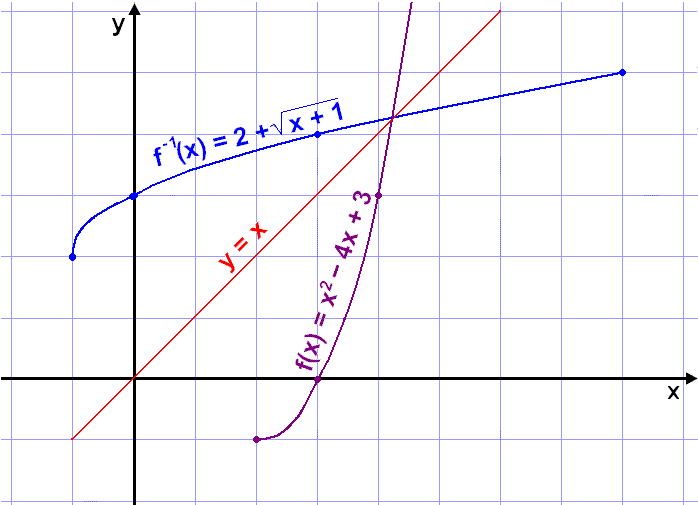
We note that the two graphs are mirror images of each other in the line  y = x. (the line that bisects the angle between the x and y axes). We can also see this from the table of values. Each point on f(x) is the mirror image of a point on  
f –1(x). For example (2, –1)  is on f(x) and (–1, 2)  is on f –1(x).  (3, 0) is on f(x) and (0, 3) on f –1(x). In general if (a, b) is on one graph then  (b, a) is on the graph of the inverse function. 

 

The graph of a function and it's inverse function are always the mirror image of each other in the line y = x.

Example 4

Look at the function f(x) = ex and its inverse function g(x) = ln x.

The function  f(x) = ex  can take any value of x so its domain is  all the real numbers R.
The values that   f(x) = ex take are always positive so it's range is the interval .
The function  g(x) = ln x  can only take positive values of x , so it's domain is .
On the other hand the function g(x) = ln x gives all real number values so it's range is R.

The Range of a function is the same as the Domain of it's inverse and the Domain of a function is the Range of its inverse.

The graphs of the two functions are shown below. Notice that they are mirror images of each other in the line y = x .

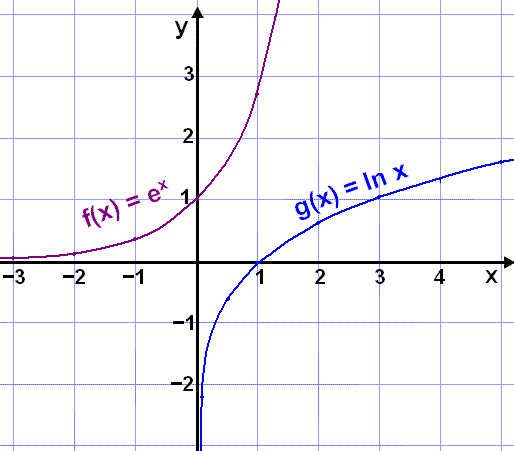
Example 5

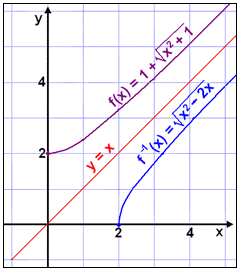
Find the interval on which the function  is increasing. Choosing this interval as the domain find the equation of its inverse function then draw both graphs in the same coordinate system.

Differentiate, using the chain rule,  to find where the function is increasing and where decreasing,

         

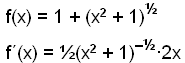
The denominator is always positive so its the x in the numerator that tells us where the function is increasing or decreasing.

The function is increasing for non negative values of x so we choose the domain

Df =

Next we solve for x to find the inverse.

             y = 1 + (x2 + 1)½

       y – 1 = (x2 + 1)½

   (y – 1)2 = x2 + 1

            x2 = (y – 1)2 – 1

                = y2 – 2y + 1 – 1

                = y2 – 2y

   

 ( choosing the positive value for x )

The inverse function is  

The graphs of f(x), f –1(x) and the line  y = x look like this.

Example 6

Find the inverse of the function  and draw the graphs in the same coordinate system.

The graph has a vertical asymptote  x = 1 and a horizontal asymptote y = 2. The domain does not contain x = 1.

We differentiate to find the slope of the graph.

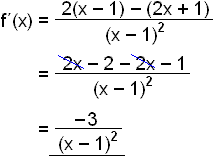
The denominator is always positive and the numerator always negative which means that the slope of the graph is always negative. So the function is decreasing on all it's domain.

We find the inverse function by solving for x.  

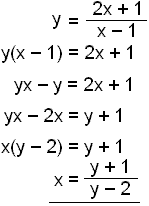
The inverse is

First get rid of the fractions then move all the terms with an x over to the left hand side of the equation. 

Now x can be factorised out .

We see that y cannot be 2.

 

This function has a vertical  asymptote  in   x = 2 and a horizontal asymptote in y = 1. This is the exact opposite to f(x) which has a vertical asymptote in x = 1 and a horizontal asymptote in y = 2.

Look at the two graphs.

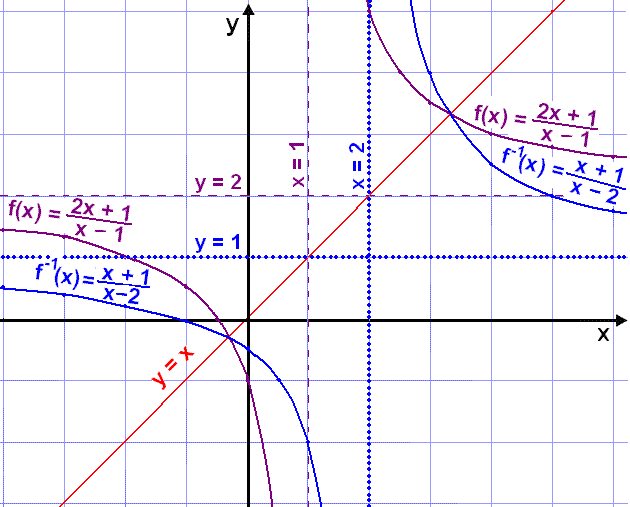
The graphs and their asymptotes are mirror images of each other in the line y = x.

 

Practise these methods and then take test 6 in functions 2.

ps. Remember the check list!