© 2009  Rasmus ehf    og Jóhann Ísak

Functions 2

Lesson 3

Rational functions and Asymptotes

A function of the form where t(x) and n(x) are polynomials is called a rational function.

The graphs of rational functions can be recognised by the fact that they often  break into two or more parts. These parts go out of the coordinate system along an imaginary straight line called an asymptote.

Let's look at the function   

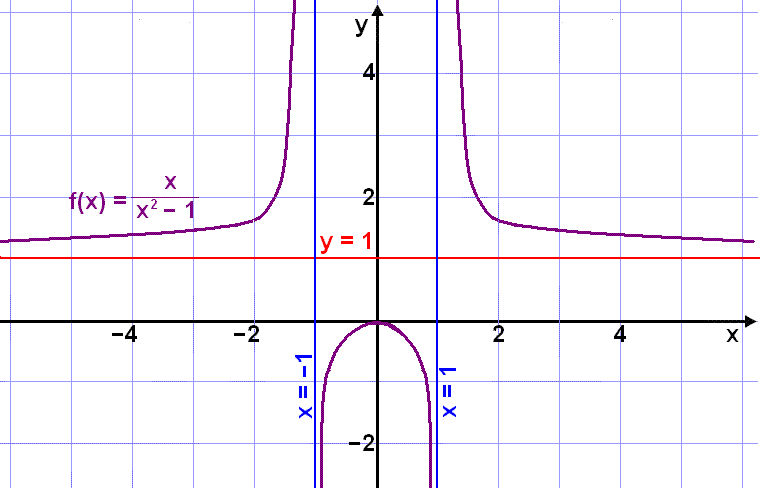
This graph follows a horizontal line ( red in the diagram)  as it moves out of the system to the left or right. This is a horizontal asymptote with the equation y = 1. As x gets near to the values 1 and –1  the graph follows vertical lines ( blue). These vertical asymptotes occur when the denominator of the function, n(x),  is zero ( not the numerator).
To find the equations of the vertical asymptotes we have to solve the equation:

   x² – 1 =  0

         x² = 1

          x = 1 or x = –1

Near to the values x = 1 and x = –1 the graph goes almost vertically up or down and the function tends to either +∞ or –∞.

We get a horizontal asymptote because the numerator and the denominator,  t(x) = x² and n(x) = x² – 1 are almost equal as x gets bigger and bigger.
If, for example, x = 100 then x² = 10000 and x² – 1 = 9999 , so that when we divide one by the othere we get almost 1. The bigger the value of x the nearer we get to 1.

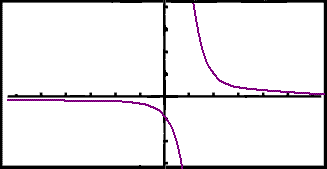
Example 1

Find the asymptotes for the function .

To find the vertical asymptote we solve the equation

   x – 1 = 0

         x = 1

The graph has a vertical asymptote with the equation  x = 1.

To find the horizontal asymptote we calculate   .

The numerator always takes the value 1 so the bigger x gets the smaller the fraction becomes. For example if x = 1000 then  f(x) = 001. As x gets bigger f(x) gets nearer and nearer to zero.

This tells us that  y = 0 ( which is the  x-axis ) is a horizontal asymptote.

Finally draw the graph in your calculator to confirm what you have found.

Example 2

Find the asymptotes for  .

We can see at once that there are no vertical asymptotes as the denominator can never be zero.

   x² + 1 = 0

         x² = –1 has no real solution

Now see what happens as x gets infinitely large:

The method we have used before to solve this type of problem is to divide through by the highest power of x.

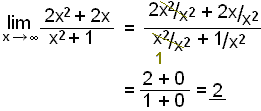	Divide all through by x2 and then cancel
	fractions where x is in the denominator and not the numerator tend to 0.

The graph has a horizontal asymptote y = 2.

Now lets draw the graph using the calculator

 First choose GRAPH  in the menu.

Then enter the formula being careful to include the brackets as shown

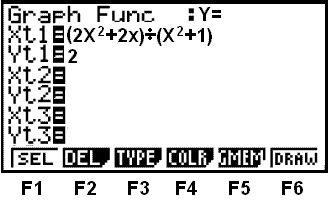
This is what the calculator shows us. The graph actually crosses its asymptote at one point. (This can never happen with a vertical asymptote).

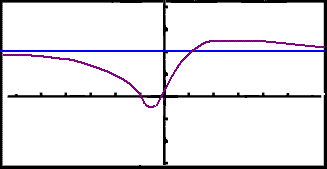
Example 3

Now an example where the numerator is one degree higher than the denominator.

  . The numerator is a second degree polynomial while the denominator is of the  first degree.

First the vertical asymptotes:

   x – 1 = 0

         x = 1        

One vertical asymptote with the equation  x = 1.

We use long division and divide the numerator by the denominator

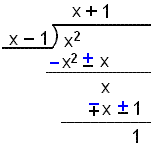
We can now rewrite f(x):

We know that   which means that  f(x) ≈ x + 1 as x gets bigger.

telling us that the straight line  y = x + 1 is a slanting asymptote

The graph is shown below.

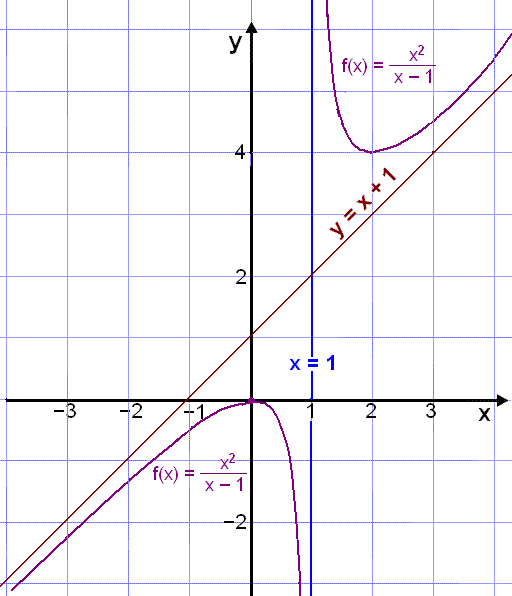
If we want to speculate on further possibilities we can see that if the degree of the numerator is 2 degrees greater than that of the denominator then the graph goes out of the coordinate system following a parabolic curve and so on.

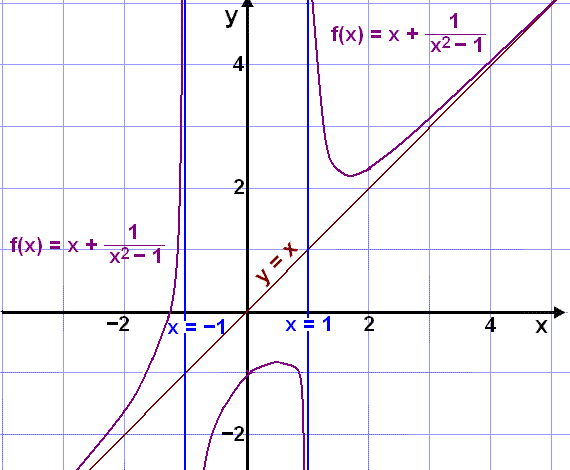
Example 4

Find the asymptotes of the function .

In this example the division has already been done so that we can see there is a slanting asymptote with the equation  y = x.

To find the vertical asymptotes we solve the equation  n(x) = 0.

   x² – 1 = 0

         x² = 1

          x = 1 or x = –1

The vertical asymptotes are x = 1 and x = –1.

Here's the graph