© 2008  Rasmus ehf    og Jσhann Νsak

Functions 2

Functions 2

Combining functions

 

There are many ways in which functions can be combined. We will be looking at some of these ways in the following.             

Example 1

Given the functions f(x) = x2 + x and g(x) = x + 1.

a)   Find the sum of f and g.

          f(x) + g(x) = (x2 + x) + (x + 1) = x2 + 2x + 1

 

b)   Find the difference between  f and g.

          f(x) – g(x) = (x2 + x) – (x + 1) = x2 + x –x – 1 = x2 – 1

 

c)   Find 2f(x) – 3g(x).

          2f(x) – 3g(x) = 2(x2 + x) – 3(x + 1) = 2x2 + 2x – 3x – 3

                               = 2x2 – x – 3

 

d)   Multiply f and g together.

          f(x)·g(x) = (x2 + x)·(x + 1) = x3 + x2 + x2 + x = x3 + 2x2 + x

 

e)   Divide  f by g.

        

        

The answer in part e) is the straight line y = x. Note however that the domain of the function  f(x)/g(x) = x cannot contain the value  x = –1 because that would involve dividing by zero.  If the domains of both f and g are all the real numbers, that is the set R, then the domain of   f(x)/g(x) = Df/g = R\{–1}. The graph of f(x)/g(x) will therefore be a straight line  y = x with a hole where  x = –1.

Now we will see how we can work out what happens if we apply one function, say g on the variable x and then apply a second function, say f, on the outcome. Combining functions f and g in this way is called function composition written f(g(x)) (read f of g of x) or f o g . f o g is called a composite function.

The following is an example where the function g is applied first to x then the function f is applied to the outcome.

Example 2

Given the functions f(x) = x2 + x and g(x) = x + 1.

a)  Find f(g(x)).

        f(g(x)) = f(x + 1) =  (x + 1)2 + (x + 1) = x2 + 2x + 1 + x + 1 = x2 + 3x + 2

b)  Now find  g(f(x)).

        g(f(x)) = g(x2 + x) =  x2 + x + 1

c)   Find  f(f(x)).

        f(f(x)) = f(x2 + x) = (x2 + x)2 + (x2 + x) = x4 + 2x3 + 2x2 + x

d)   Find g(g(x)).

        g(g(x)) = g(x + 1) =  (x + 1) + 1 = x + 2 

In the composite function  f(g(x)), g(x) is called the inner function and f(x) the outer function. When we combine functions the inner functions comes in place of the variable in the outer function.

Example 3

Given the functions  f(x) = and  g(x) = x2 + 1.

a)  Find f(g(x)).

        f(g(x)) = f(x2 + 1) =

b)  Find g(f(x)).

        g(f(x)) = g()= = x + 1

We have already looked at the translation of functions. We can also look at translations as composite functions. Look at the next example.

Example  4

We wish to translate the graph of the function f(x) = x3 – x by the vector  .

The following table of values is for x taking values between  –2 and 2. First we calculate f(x). Next we move all the outcomes down by 1 ( e.g. the value for x = – 2 becomes the value for x = –1). This is equivalent to calculating the values of f(x–1). Finally we add 3 to all the outcomes .

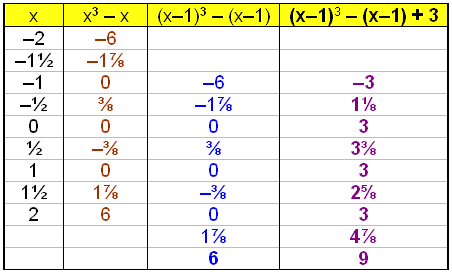
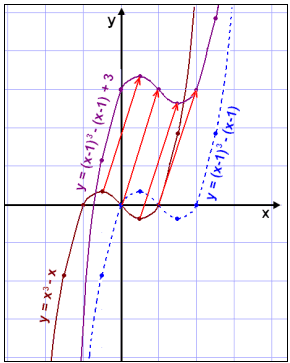
We can see from the diagram that translating the graph of f(x) one unit to the right gives us the graph of   f(x–1)  (see the blue graph). When 3 is added  to the blue graph it moves up by three units. So each point on the original graph f(x) has been translated by the vector .

The following ruke therefore applies:

Translating the graph f(x) by the vector

gives us the graph f(x–a) + b.

Example 5

We now look at the functions  f(x) = and g(x) = 4 – x2 and find the domain and range of their composite functions.

We obviously have to limit the values under the squareroot sign to non negative numbers only. Therefore the composite function  f(g(x)) = can only take the positive values that we get from the function g(x) = 4 – x2 . This means we have to limit the domain of the inner function g(x) so that the range (outcome) of the function will only be non negative numbers.  Look at the graph of  g(x) = 4 – x2 with this in mind. The table of values is as follows:

 

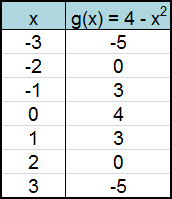
This is what the graph looks like

.

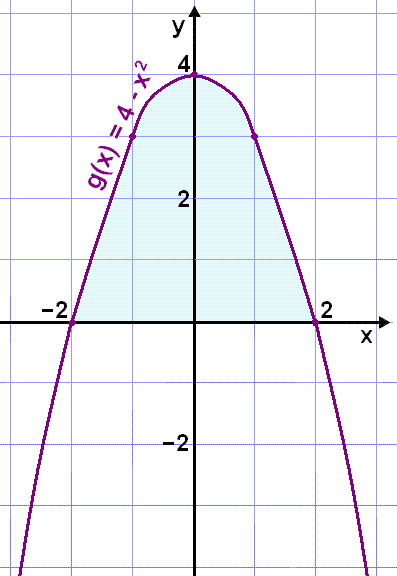
The shaded area of the graph shows where g(x) lies above the  x axis. On the interval between –2 and 2  the inner function g(x) takes the non-negative values 0 to 4.

If we choose the domain of g(x) or Dg(x) = {x R | –2 x 2} we get the range Rg(x) = {y R | 0 y 4}. This set must then be the domain of f(x) in the composite function.  If we choose values for x on the interval 0 x 4,  f(x) takes values between 0 x 2.

We have shown that the domain of f(g(x)) is Df(g(x)) = {x R | –2 x 2} and the range og f(g(x)) is Rf(g(x)) = {y R | 0 x 2}. Finally look at the graph.

First the table of values.

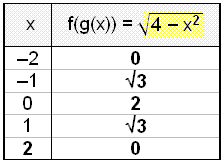
The graph is a semicircle with centre (0, 0) and radius 2.

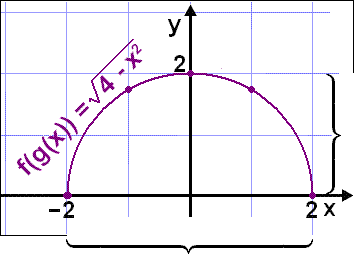Rf(g(x)) = {y R | 0 x 2},

         Df(g(x)) = {x R | –2 x 2

 

Here are some points to follow when finding the domain and range of a composite function.

1)   Choose the domain of the inner function so that the range
      is valid to use as the domain of the outer function.    

2)  Using this domain find the range of the outer function.

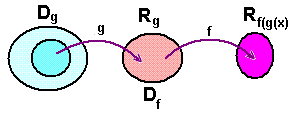
Sometimes, as in the above example, only part of the domain of g can be used. The range of values that g takes using this domain becomes the domain of the outer function f.  The values that f takes using this domain will be the range of the composite function f(g(x)).

Practise these methods and then take test 1 in functions 2.

ps. Remember the check list!