Functions I
| © 2007 Rasmus ehf and Jóhann Ísak |
Functions I |
Lesson 2
Polynomials
The following functions are examples of polynomials:
| Degree |
f(x) |
Graph example: |
|
0 |
f(x)
= a Coefficient: a |
|
|
1 |
f(x)
= ax + b |
|
|
2 |
f(x)
= ax2
+ bx + c |
|
|
3 |
f(x)
= ax3
+ bx2
+ bx + c |
|
|
4 |
f(x)
= ax4
+ bx3
+ cx2
+ dx + e |
|
|
E.t.c |
||
The coefficients a, b, c, e.t.c. are known constant numbers that determine the shape of the polynomial. x is a variable for which we can choose values.
The highest power of x that appears in the polynomial is called the “degree” of the polynomial.
We write the expression with the highest power of x first then the others in descending order.
If any power of x is missing it is because the coefficient of that x is zero.
If no coefficient is visible in front of one of the terms then that coefficient is 1.
Example 1
Find the degree of the polynomial f(x) = x5 − 2x3 + 4x − 5 and it’s coefficients:
The highest power of x is 5 so this is a polynomial of degree 5.
x4 and x2 are missing so their coefficients are 0.
x5 has no visible coefficient so it is 1
We can think of the
term without an x as being x0,
as all numbers to the power 0 equal
1. Now we can rewrite this polynomial and note the coefficients.
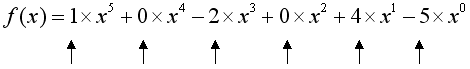 |
||||||
| Coefficients: |
1 |
0 | -2 | 0 | 4 | -5 |
Notice a polynomial of degree 5 has 6 coefficients. The number of coefficients is always one more than the degree of the polynomial
The powers in a polynomial are always whole, positive numbers or zero. (In the set N0). The following functions are not polynomials:
|
f(x) = x2 + x + 1 + x−1 + x−2 |
(a negative power of x) |
|
g(x) = x2
+ x + 1 + |
(x is under a square root) |
|
h(x) = x2 + x + 1 + 2x |
(x is a power) |
|
|
(x is in the denominator) |
If you look at the graphs of the polynomials above you will see that a polynomial of degree 0 is a horizontal line.
A first degree polynomial has a sloping line graph.
A second degree parabola has a graph called a parabola. It has one turning point.
A third degree is a bit like two parabolas joined together, one of them opening up and the other opening down. It can have two turning points
A fourth degree resembles three parabolas joined together with a maximum of three turning points, and so on.
As the degree of the polynomial increases the possible number of turning points increases. The maximum number of turning ponts is always one less than the degree of the polynomial.
It follows also that a first degree polynomial crosses the x axis only once, a second degree polynomial crosses the axis at the most twice, a third degree up to three times and so on.
(look at the graphs again).
The constant term ( the term without an x) tells us where the graph crosses the y axis. This is because x = 0 on the y axis and if we put x = 0 into the equation we are left with only the constant term.
When f(x) = 2x3 + 3x2 + 4x + 6
f(0) = 2×03 + 3×02 + 4×0 + 6 = 6
The point (0, 6) is the point where the graph crosses the y axis .
All points on the x axis have the y−value zero so we can find where the graph crosses the x−axis by putting y = 0 and solving the equation for x. y = f(x) = 0.
Example 2
Find the points where the polynomial f(x) = 2x + 4 crosses the x and y axes. We call these the x-intercept and the y-intercept.
| y-intercept: is 4. | The constant in the formula for f(x) is 4. |
| x-intercept: 2x + 4 = 0 | Put f(x) = 0. |
| x = −4/2 = −2 | Solve for x. |
| So the x-intercept is −2. |
Example 3
Find the points of intersection of the polynomial
f(x) = x2 − 2x with
the x and y axes.
| y-intercept is 0. | The constant term is 0. |
| x2 − 2x = 0 | Put f(x) = 0. |
| x (x − 2) = 0 | Factorise and solve for x. |
The polynomial intersects the x axis in two points, x= 0 and 2.
Example 4
Find the points of intersection of the polynomial
f(x) = (x − 1)(x − 2)(x − 3) with the x and y axes.
If we examine the equation we can see that when we multiply the brackets together the constant term will be -6.
If you don´t spot this then you can find the constant by multiplying the brackets together.
(x − 1)(x − 2)(x − 3) = (x2 − 2x − x + 2)(x − 3)
= (x2 −3x + 2)(x − 3)
= x3 − 3x2 − 3x2 + 9x + 2x − 6
= x3 − 6x2 + 11x − 6
Or another simpler way to find this point of intersection is by calculating f(0) without multiplying the brackets together.
f(0) = (0 − 1)(0 − 2)(0 − 3) = −6
The y – intercept is where y = −6.
To find where the graph crosses the x axis we have to solve the equation
(x − 1)(x − 2)(x − 3) = 0
The only way for this multiplication to be zero is if one of the factors ( brackets ) is zero . This happens when x = 1, 2 or 3. Therefore we see that the graph crosses the x axis when x=1, x=2 and x=3.
Example 5
Do the points (1, 6) and (2, 8) lie on the graph
of the function
f(x) = x2 + 4x + 1 ?
| f(1) = 12 + 4×1 + 1 | Calculate the value of f(1). |
| = 1 + 4 + 1 = 6 |
It follows that (1, 6) lies on the graph.
f(2) = 22 + 4×2 + 1
= 4 + 8 + 1 = 13
Therefore (2, 8) is not on the graph.
Example 6
Find the equation of a first degree polynomial (a straight line) that goes through the points (1, 1) and (2, 3).
Let’s call the function f(x) = ax + b
Putting in the values (1, 1) we get the equation
f(1) = a×1 + b = 1 or a + b = 1
Putting in the values (2, 3) we get the equation
f(2) = a×2 + b = 3 or 2a + b = 3
f(2) − f(1) = (2a + b) − (a + b) = 3 − 1
|
= 2a + b − a − b = 2 a = 2 2 + b = 1 b = 1 − 2 = −1 |
Solve the simultaneous equations
a + b = 1 |
The equation of the polynomial (line) is f(x) = 2x − 1.
Example 7
Find a second degree polynomial
(parabola) whose graph goes through the points (0, 6), (1, 0) and (3, 0).
Call the function f(x) = ax2 + bx + c and calculate a, b and c.
((0, 6) is the y-intercept so c = 6.
f(1) = a×12 + b×1 + 6
| f(3) = a×32
+ b×3 + 6 = 0 = 9a + 3b + 6 = 0 3a + b + 2 = 0 |
Simplify
the equation by dividing through by 3 |
f(3) = f(1) = 0
3a + b + 2 = a + b + 6
3a − a + b − b = 6 − 2
2a = 4
a = 2
f(1) = 2 + b + 6 = 0
b = −2 − 6 = −8
Therefore the polynomial is f(x) = 2x2 − 8x + 6
Try Quiz 2 on Functions I.
Remember to use the checklist to keep track of your work.