© 2008 Rasmus ehf
and Jóhann Ísak
Trig functions
© 2008 Rasmus ehf |
Trig functions |
|
Solve the equation sin x = cos x and then the inequality
sin
x > cos x on the interval 0 
x < 2
.
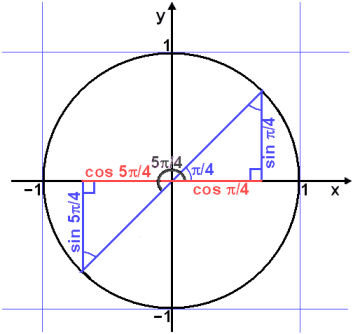
From the unit circle we see that sin x and cos x
can only have the same value in two places, in x = /4
and x = 5/4
(45° and 225°).
The equation sin x = cos x can also be solved by dividing through by cos x.
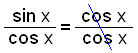
tan x = 1
x = tan−1(1)
x = 45°∙ /180°
+ k∙
x = /4 + k∙ (k is any whole number, positive or negative)
If we put k = 0 and k = 1 we get the solutions /4 (45°)
and /4 + = 5/4 (45°+
180°= 225°).
To solve the inequality sin
x > cos x we need to see which is the greater sin x or cos x on the intervals
between the solutions /4
and 5/4.
The solutions can be seen if we draw the graphs of f(x) = sin x and g(x) = cos
x. The graph of sin x lies above the graph of cos x on the interval /4 x 5x/4 (see the shaded area in the diagram).
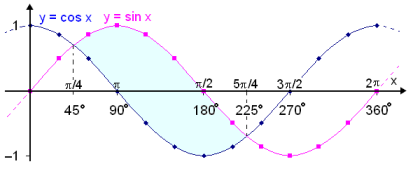
sin x 
cos x on the interval /4 x 5x/4.
Solve the equation sin x ∙ cos x = 0 and then the inequality
sin x ∙ cos x > 0 on the interval 0 x < 2.
The inequality has no solution when sin x or cos x take the value 0. This happens at intervals of 90°.
The solutions of the
equation sin x ∙ cos x = 0 on the interval 0 x < 2 are therefore 0, /2, and 3/2 (0°, 90°, 180°
and 270°).
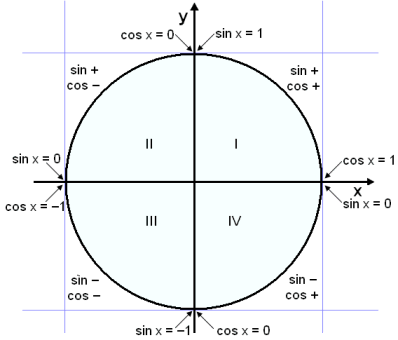
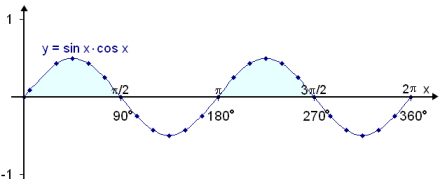
The solution of sin x
∙ cos x > 0 can be found by looking at the unit circle. We need to find
where sin x multiplied by cos x is positive. In other words sin x and cos x have
to have the same sign, both be
positive or both negative. This occurs in the first and third quadrant. The
solutions are therefore
0 < x < /2 and p < x < 3/2.
We can also see this by
plotting the graph of
f(x) = sin x ∙ cos x.
Solve the equation sin x
∙ cos x − sinx = 0 and then the inequality sin x ∙ cos x
− sin x > 0 on the interval 0 x < 2.
sin x ∙ cos x − sinx = 0 sin x (cos x − 1) = 0 |
We need to factorise the equation by taking sin x outside a bracket. |
The equation has solutions when sin x = 0 or when the bracket, (cos x − 1) = 0.
sin x = 0
x = 0 or (180°).
or
cos x − 1 = 0
cos x = 1
x = 0
The only solutions of the
equation are therefore 0 and .
The inequality sin x ∙ cos x − sin x > 0 can be rewritten as sin x (cos x − 1) > 0.
Now it’s useful to make a table of signs and look at the signs of sin x and cos x − 1.
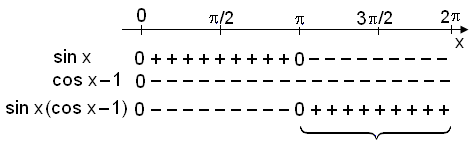
Solution
We see that both factors are
negative on the interval
< x < 2.
Now, lets see how this fits
in with the graph of
f(x) = sin x ∙ cos x − sin x
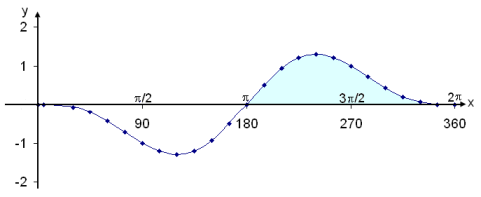
The shaded area above the x
axis shows where
sin x (cos x − 1) > 0, which agrees with our calculations.
Find all solutions of the equation cos2 x − cos x = 0.
cos2 x − cos x = 0
cos x∙(cos x − 1) = 0
Solutions can be found when cos x = 0 or cos x − 1 = 0
cos x = 0
x =/2 or 3/2 (90°
or 270°)
x = /2 + k∙
or
cos x − 1 = 0
cos x = 1
x = 0 + k∙2 = k∙2
All solutions fit into the pattern x = /2 +
k∙
Find all solutions of the equation sin2 x − 5 sin x + 4 = 0.
This is a quadratic equation with sin x as the variable. We can therefore solve for sin x using the quadratic formula. a = 1, b = −5 og c = 4.
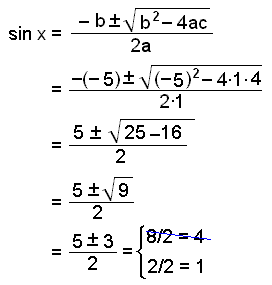
Sine we cannot take the value 4 therefore we do not need to consider sin x =
4. The other possibility is sin x = 1 which has the solution
/2 (90°). The complete solution is therefore:
x
= /2 +
k∙2
Solve the equation sin 5x° = sin x°.
One possibility is that the position of 5x° on the unit circle is the same as the position of x° and as this position repeats itself at intervals of 360° we get the following equation:
1) 5x° = x° + k∙360°
4x° = k∙360°
x° = k∙90°
We show this possibility in the diagram.
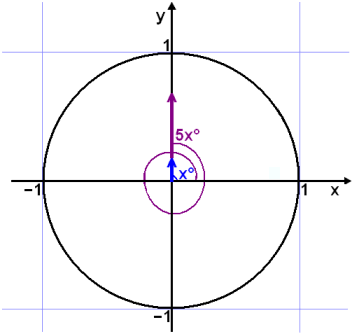
A second possibility comes
from the fact that
sin x° = sin (180°
− x°). This gives us the following solution:
5x° = 180° − x° + k∙360°
6x° = 180° + k∙360°
x° = 30° + k∙60°
This solution is shown in the diagram to the right.
But we notice that the first solution is contained in the second solution so it is sufficient to give the second solution
x° = 30° + k∙60°
Solve the equation cos 2x =
cos x on the interval 0 x < 2.
1) First we consider the possibility that x and 2x are in the same position on the unit circle.
2x = x + k∙2 x = k∙2 x = 0 |
Subtract
x from both sides of the equation and then choose k = 0 (k = 1 gives 2 |
2) The second possibility comes
from the fact
cos v = cos (−v). The solution is then as follows:
2x = −x
+ k∙2
3x = k∙2
x = k∙2/3
This gives the solutions 2/3 (120°)
for k = 1 and 4/3 (240°) for k = 2. The
complete solution is therefore:
0, 2/3 og 4/3.
Solve the equation tan 3x = tan 2x.
Tan equations are in many ways the easiest of the trig equations as there is only on possibility to consider that repeats itself at intervals of 180°.
3x = x + k∙180°
2x = k∙180°
x = k∙90°
or in radians
x = k∙/2
Try Quiz 5 on Trig functions.
Remember to use the checklist to keep track of your work.