© 2008 Rasmus ehf
and Jóhann Ísak
Trig functions
© 2008 Rasmus ehf |
Trig functions |
|
We begin by looking at a right angled triangle where the hypotenuse has a length of 1 unit.
 |
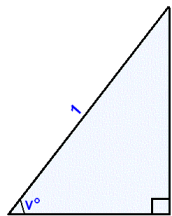Opposite side = sin v° |
Adjacent side = cos v° |
In a right angled triangle
sin v° = opposite side/hypotenuse
and
cos v° = adjacent side/hypotenuse.
If the hypotenuse in a triangle has length 1 then it follows that
sin v° = opposite side and cos v° = adjacent side.
We now consider a circle drawn in a coordinate system.
A circle with a radius of 1 unit and it’s centre in (0, 0) is called the Unit circle.
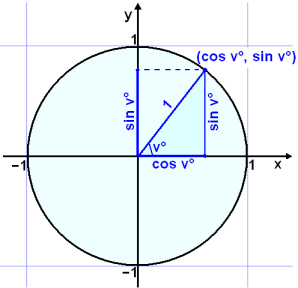The Unit circle
If we draw a radius that makes an angle of v° with the positive arm of the x axis and drop a perpendicular as the diagram shows we get a right angled triangle with sides of length cosv° and sin v°. This means that the coordinates of the point where the radius intersects the circle must be (cos v°, sin v°).
Now we’ll look at tan v° a similar way.
 |
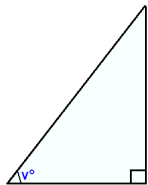opposite side = tan v° |
Adjacent side = 1 |
This time we choose the adjacent side to be of length 1 unit.
tan v° = opposite side/adjacent side.
The adjacent side = 1 therefore tan v° = opposite side.
We can add this to the diagram of the unit circle.
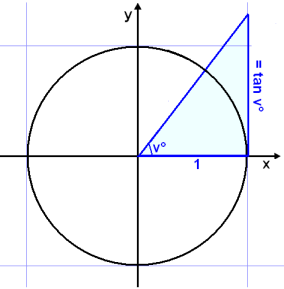
To see the connection between sin, cos and tan we do the following calculations:
opposite side
tan v° =
adjacent side
opposite side/hypotenuse |
Dividing the numerator and denominator by the hypotenuse. |
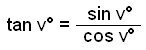
The calculations we have shown so far apply to an
angle drawn in the unit circle, measured from the x – axis and lying in the
first quadrant of the coordinate system. If we call the point where the radius r cuts the
circle P, and rotate the radius OP anticlockwise round the circle from the x
axis we say that the angle v° is a
positive rotation. If OP is rotated clockwise from the x axis we
talk about a negative rotation. ( this is simply a definition that has been agreed on). So if P moves along the circle up from the x axis we
have a positive value for the rotation v. If P moves along the circle and down
from the x axis we have a negative value for v.
( see the diagram).
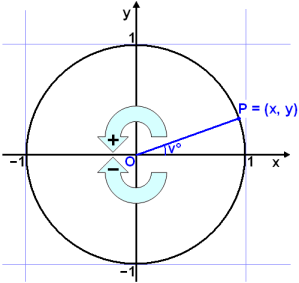
We now generalise the definition of sine, cosine and tangent as follows:
cos v° = x-coordinate of P sin v° = y-coordinate of P |
This definition implies that the trig functions can be positive or negative depending on in which quadrant of the coordinate system the point P lies.
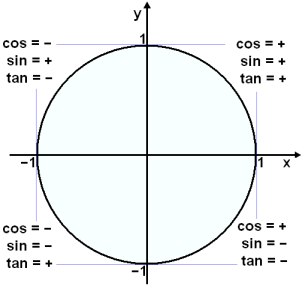
As the point P moves with a positive rotation round the circle it reaches the same position every 360° . This means that the values of sine and cosine are repeated every 360°. Tangent repeats it’s value every 180° as we will see in example 4.
Find the positive rotation that takes us to the same position as −200°
To do this we simply have to add on 360°.
−200° + 360° = 160°
Find an angle on the
interval 0°
v° < 360° equivalent
to 1100°.
We need to subtract 360° several times until we reach the interval required.
1 circle: 1∙ 360° = 360°
2 circles: 2∙ 360° = 720°
3 circles: 3∙ 360° = 1080°
This is sufficient.
1100° − 1080° = 20°
We will now see how Pythagoras can be use to calculate some exact values for the trig functions.
First we look at 30°. The triangle in the diagram is half of an equilateral triangle and therefore we know that the opposite side is ½.
 |
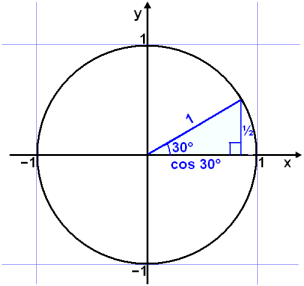sin 30° = ½ = 0,5 cos 2 30° + (½)2 = 12 cos 2 30°= 1 − ¼ = ¾
≈ 0.866 |
Pythagoras rule |
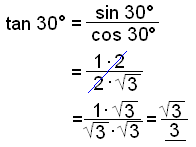
≈ 0.577
Next we look at the angle 45°. The triangle is isosceles, we call the sides a.
 |
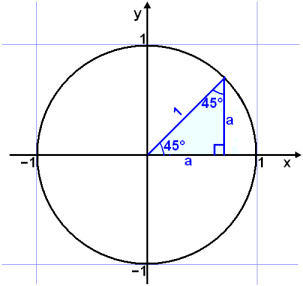a2 + a2 = 1 2a2 = 1 a2 = ½ |
 |
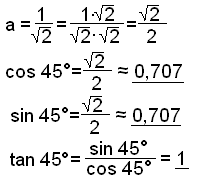Now the angle 60°.
 |
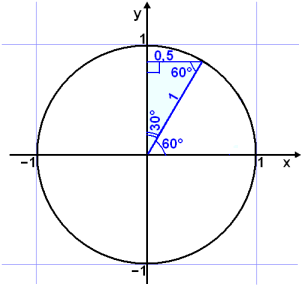Again we have a triangle with 30°, 60° and 90° so we can use the same calculations as for 30°. Notice that sine and cosine have exchanged values. |
 |
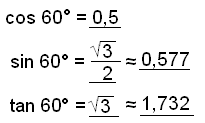The values of the trig functions for 90° can easily be seen from the unit circle. OP, the arm of the angle lies on the y axis so the x-coordinate is 0 and the y coordinate is 1.
cos 90° = 0
sin 90° = 1
tan 90° = 1/0 does not exist.
Angles that are in other quadrants can be found by comparing them with angles in the first quadrant.
 |
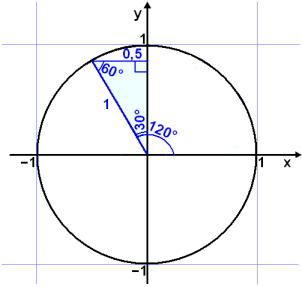120° lies in the second quadrant (to the left of the positive y – axis) and therefore the cos 120° is negative, but the sin 120° is positive.. |
 |
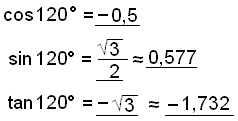We can continue in this way.
135° (90°+ 45°) or ( 180°− 45°) can be found from 45°, only the signs change.
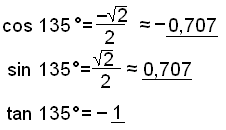
Find the values of sine, cosine and tan for 225°.
225° is in the third quadrant and can be calculated from 45°. (45° + 180° = 225°). We begin by drawing a diagram.
 |
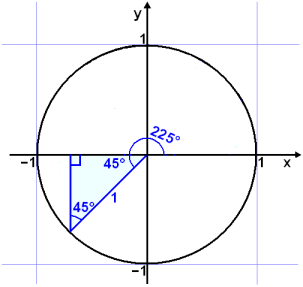We calculate in the same way
as in example 3, both sine and cosine are negative but tan is positive |
 |
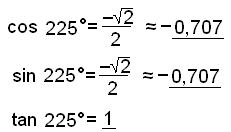Notice that tan 225°is the same as tan 45°. In other words the value of tan v° repeats itself every 180°.
Find all the solutions of the equation tan x° = 2, then write down which of these solutions are on the interval 0°
x° < 360°.
Use the inverse tan function, tan −1, on your calculator.
tan −1(2) ≈ 63.44°
We know that the values of tan repeat themselves every 180°, so we can write a formula for all the solutions by adding k∙180° where k represents any whole number. The complete solution is therefore:
x° ≈ 63.44° + k∙180° k is a whole number.
Two of these solutions lie on the interval 0°
x° < 360°. They are x° ≈ 63.44° and x° ≈ 63.44° + 180° ≈ 243.44°
Find the angles where sine takes the value 0.5 .
We first solve the equation sin v° = 0.5 using a calculator and the inverse sine function sin −1 . sin −1(0.5) = 30°. Now draw a diagram of the unit circle.
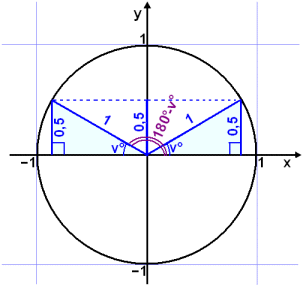
Draw the angle v° as
usual starting from the positive x axis and turning anticlockwise. The y
coordinate of the point on the circle (height above the x axis ) is sin v°.
We are given this value 0.5 (sin v° = 0.5).
If we draw a horizontal line through this point (the dotted line in the diagram) we can see that there is a second point on the circle which has the same y coordinate and therefore the same value of sine. Both the shaded triangles in the diagram are congruent ( exactly the same). Measuring the rotation of this second radius from the positive x axis we get the second answer for v:
v°= 180° − 30° = 150°.
From this example we get the following rule:
| sin v° = sin (180°-v°) |
We use this rule when we need to solve equations of the type
sin v° = a
Unfortunately calculators
only give us one solution, the smallest angle that satisfies the equation
measured from the positive x axis. We find the second answer by
subtracting this answer from 180°. To find all possible solutions we need to
add k∙360° to both solutions.
( k can be any whole number ).
Find all the solutions of the equation sin v° = −0.6.
Draw a diagram of the unit circle to see what we need to do.
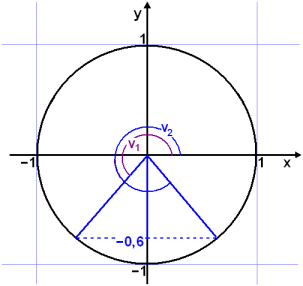
The calculator gives one solution sin −1(−0.6) ≈ −36.9°.
We get the second answer by subracting from 180°.
180° − (−36.9°) ≈ 216.9°
Add 360° to −36.9° to get rid of the negative.
−36.9° + 360° ≈ 323.1°
The complete soution is: v1 ≈ 216.9° + k∙360° og v2 ≈ 323.1° + k∙360°
( It’s a good idea to use your
calculators to check the answers.
sin 216.9° ≈ −0.6 and
sin 323.1° ≈ −0.6 )
Solve the equation cos v° = 0.7.
Draw the unit circle to see what solutions there are.
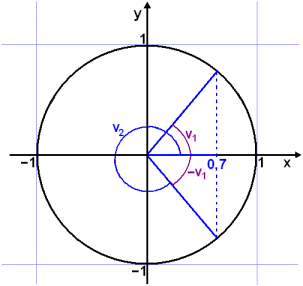
In this example we are given the x coordinate ( cos v°= 0.7) of the point on the circle, that is the distance from the y axis. A perpendicular line ( dotted line) through the point where the radius intersects the circle has been drawn. This perpendicular line through 0.7 on the x axis cuts the circle in two points telling us there are two angles where cos v°= 0.7.
Using the calculator we get cos −1(0.7) ≈ 45.57°. We can see that the second angle is −45.57° . We find the positive angle equivalent to this by adding 360°.
Solutions: v1 ≈ 45.57° + k∙360°
v2 ≈ −45.57° + 360° + k∙360° ≈ 314.43° + k∙360°
From this example we can see the following rule.
| cos v° = cos(-v°) |
This is the rule we use to solve equations of the type
cos v° = a
The calculator gives one answer, the second answer is the negative of the first answer. We can always convert negative answers to positive by adding 360°. Finally we find all solutions by adding k∙360° to each answer.
Solve the inequality cos v° < −0.7 on the interval 0°
v° < 360°.
First we solve the equation cos v° = −0.7.
The calculator gives cos −1(−0.7) ≈ 134.43° . The second solution is therefore −134.43° or −134.43 + 360° ≈ 225.57°. Now we need to draw the unit circle.
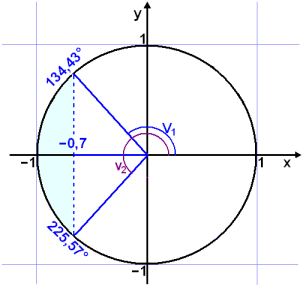
We can see that cos v° is less than −0.7 if v° is in the shaded area on the diagram.
The solution is therefore 134° < v°< 226°.
Try Quiz 2
on Trig functions.
Remember to use the checklist to keep track of your work.
