Statistik
© des. 2003 Rasmus.is
Introduktion 4.
Histogram,
frekvens spridning, urval, vägt medelvärde:
Frekvensspridning
Studera hur mycket 30 elever väger
i kg. Alla eleverna går i 10:e klass och de sorteras efter vikt, de
lättaste först o.s.v.
50, 52, 54, 55,
57, 57, 58, 60, 60, 60, 61, 61, 62, 62, 63,
64, 65, 66,
66, 67, 67, 67, 67, 68, 70, 70, 71, 72, 73, 74
Ofta samlas mätningar i grupper.
Vi väljer att ha 5 kg imellan grupperna.
|
Gör en frekvenstabel.
|
| Vikt
i kg. |
Frekvens |
| 50
- 54 |
3 |
| 55
- 59 |
4 |
| 60
- 64 |
9 |
| 65
- 69 |
8 |
| 70
- 74 |
6 |
Histogram
|
|
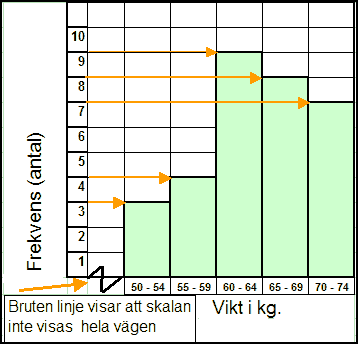
Rita sedan frekvensspridningen med
ett histogram.
Histogrammet visas för
valda tal. Men ingen i gruppen var lättare än 50
kg tas den del av skalan inte med. Detta visas med en bruten
linje.
Histogram har täta staplar
som ligger ihop och alla måste vara lika breda. |
Av bilden kan utläsas att 3 av dessa
30 är (50 till 54 kg.) eller 10% av gruppen.
Urval:
Om stor mängd information skall
undersökas är det vettigt att använda statistik. Nu vill
vi undersöka tillgång till internetet hos elever i 10:e klass
i en stad. Det är inte tid för att fråga varje elev om tillgång. Vi talar med 100 elever valda slumpmässigt ur grundskolan.
Det totala antalet elever i 10:e är 4500 i denna stad, urval är därför
100 elever. I urvalet är 50 pojkar och 50 flickor.
Vi frågar följande frågor:
Resultaten är följande.
| Frågor
och svar |
Frekvens
(pojkar) |
(Frekvens
flickor) |
Totalt
|
| Har egen
dator |
40 |
35 |
75 |
| Har tillgång
till internetet |
45 |
40 |
85 |
| Har inte tillgång
till internetet |
5 |
10 |
15 |
Nu hade vi tur att urvalet är 100
elever, så det är enkelt att omskriva resultatet i procent.
Vi ser att 85 eller 85% av eleverna
i urvalet har tillgång till internetet och då kan vi förutsäga
om det antal elever i 10:e som har tillgång till internetet.
Enligt urvalet är det 85% av eleverna. Vi räknar därför
85% av 4500 och får att 0.85 x 4500 = 3825 . Därför kan
vi konstatera med relativ säkerhet att drygt 3800 elever i 10:e
har tilgång till internetet hemma.
Liknande metoder används till
att undersöka olika delar i vår närmaste omgivning.
Som exempel kan nämnas:
Vägt
medelvärde:
Två 10:e klasser är i
en skola. De tog nationella prov i matematik och resultatet var följande
10:e klass A medelbetyg 7,0
Antalet elever var 20
10:e klass B medelbetyg 6,0
Antalet elever var 30
Vi ska nu räkna skolans medelbetyg.
Det vore fel att addera klassernas
medelbetyg eller 7+ 6= 13 och dividera sedan med 2 och påstå
att medeltalet är 6,5 därför att det är inte samma
antal elever i klasserna.
Vägt
medelvärde.
Vi måste addera alla elevernas
betyg i båda klasserna och dividera den siffran med det totala antalet
elever i de båda klasserna.
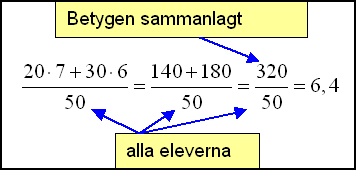
Vi räknar vägt medelvärde
genom att addera alla betygen och dividera med antalet individer. Vägt
medelvärde är 6,4 men inte 6,5
Öva på detta och gör
sedan test 4 i Statistik.
Obs ! Kom ihåg att
fylla i checklistan.


