© juli 2000 Hugo och Tomas Rasmus
Algebra - repetition
Introduction.
Här kommer några repetitionsuppgifter i algebra som kan vara bra att träna på. I Mattehjälpen finns exempel med liknande uppgifter, om du behöver förklaringar.
Exempel 1: Beräkna potensen och förenkla uttrycket:
36 + 2·8=
36 + 16 = 52
Exempel 2: Förenkla:
y + xy +2y= 3y + xy
Exempel 3: Förenkla:
xy +yx = 2xy
Exempel 4: Förenkla:
Exempel 5: Förenkla:
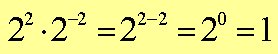
Exempel 6: Förenkla så långt som möjligt:
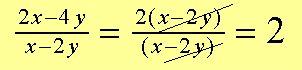
Se Faktorisering och Bråk: Multiplikation och Division.
Exempel 7: Förenkla så långt som möjligt:
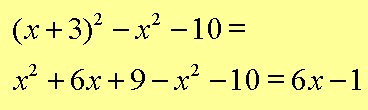
Exempel 8: Förenkla så långt som möjligt:
x +14 = 30
x = 30 - 14
x = 16
Exempel 9: Förenkla så långt som möjligt:
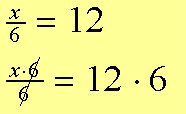
x = 72
Exempel 10: Förenkla så långt som möjligt:
5(x + 2) = - (8 - 3x)
5x + 10 = - 8 + 3x
5x -3x = -8 -10
2x = -18
x = -9
Exempel 11: Beräkna värdet av uttrycket om a=3.
21 - 36 = -15 Se Teckenregler.
Exempel 12: Förenkla så långt som möjligt:
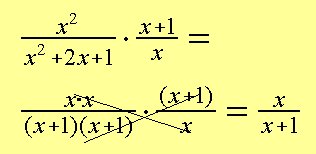
Se Bråk: Multiplikation och Division. och Faktorisering.
Exempel 13: Förenkla så långt som möjligt:
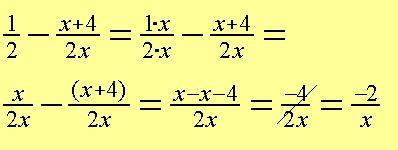
Exempel 14: Lös ekvationen:
Exempel 15: Faktorisera och beräkna möjliga värden för x och y.
Alternativ 1:
Se faktorisering
och Ekvationssystemet
(x - y)(x + y)=3·5
Då får du två påståenden
a) x - y = 3
b) x + y = 5 Du lägger ihop dessa påståenden och får då:
x + x + y - y = 3 + 5
2x=8 då x = 4
Du sätter in värdet för x i ekvationen och ser att:
4 + y = 5
y = 5 - 4
y =1
Alternativ 2:
(x - y)(x + y)=1·15
Då får du två påståenden:
a) x - y = 1
b) x + y = 15 Du lägger ihop dessa påståenden och får då:
x + x + y - y = 1 + 15
2x=16 då x = 8
Du sätter in värdet för x i ekvationen och ser att:
8 + y = 15
y = 15 - 8
y = 7
Nu kan du ge dig på det Stora Provet om du har förberett dig tillräckligt och gjort de 30 tester som kommer före. Lycka till!
