|
Tabell för y = x + 1. |
Grafen till y = x + 1 |
Exempel: 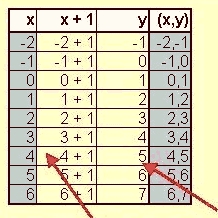 |
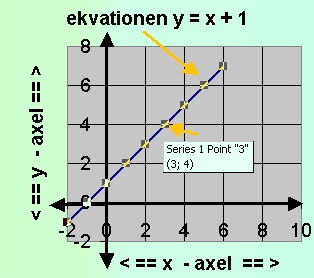 |
|
x = 4 , då blir y = 4 + 1 = 5 |
Vi ser pilen som pekar på punkten ( 3, 4) |
© mars 2000 Hugo och Tomas Rasmus
Ekvationssystemet
Introduktion 1.
En ekvation för en rät linje (linjära funktioner).
(I ett koordinatsystem som beskriver ett samband mellan variabler, är variabeln y beroende av variabeln x. En ekvation som används för att beskriva hur något är beroende av något annat kallas för funktion. En funktion vars graf är en rät linje kallas för en linjär funktion. En linjär funktion kan beskrivas med formeln: y = ax + b, där a och b är kända faktorer.)
I en linjär funktion är det tillräckligt att känna till 2 punkter
för att kunna rita grafen (linjen). Man bör dock alltid ta reda på minst 3 punkter för att
kontrollera att man räknat rätt.
När du har en linjär funktion är det bra att sätta upp en tabell över de koordinater
du räknar ut.
Sambandet mellan variablerna måste bevaras konstant, men du kan välja vilket
tal du vill i stället för x och sedan räkna ut koordinater för y.
Du väljer själva hur många koordinater du räknar ut. Du använder dock
alltid av minst 3 punkter. Om punkterna inte hamnar på en rät linje måste du
kontrollera uträkningarna för att hitta felet.
Du tar t.ex. funktionen: y = x + 1
|
Tabell för y = x + 1. |
Grafen till y = x + 1 |
Exempel:  |
 |
|
x = 4 , då blir y = 4 + 1 = 5 |
Vi ser pilen som pekar på punkten ( 3, 4) |
Du ser pilen som pekar på punkten (3,4). Det är ett exempel på en punkt som du tagit från tabellen. En annan punkt finns t. ex. på (0,1), vilken är den punkt där grafen skär y-axeln. När två sådana punkter prickats in i koordinatsystemet, är det enkelt att dra en linje mellan dem.
Andragradsfunktioner
Funktioner med formler som: y = kx2 + m där k och m är kända värden, kallas för andragradsfunktioner.
För att dra linjer för dessa ekvationer måste man pricka in fler än tre punktar.
Exempel: Du har funktionen: y = x2 - 4
Du gör en tabell för x mellan -5 till och med +5.
|
Funktionen: y = x2 - 4 |
Kurvan: y = x2 - 4 |
|
|
|
|
Exempel: x = - 4 då blir y =( - 4)(-4) -4 = 16 - 4 = 12 |
Du ser att du ibland får samma y-värde två gånger. Det beror på att andragradsfunktioner är symmetriska. |
Du ser t. ex. att punkten (4,12) har en motsvarighet i punkten
(-4,12).
Observera var kurvan skär y-axeln och x-axeln.
Om du faktoriserar uttrycket y = x2 - 4
får du y = x2 - 4 = (x-2)(x+2)
Om du väljer att y =
0, då måste x bli
+2 eller
-2 för att ekvationen ska
stämma. Då får du koordinaterna (-2,0) och
(2,0)
Riktningskoefficienten i en linjär funktion.
Studera funktionen y = 2x + 1.
|
|
Du har funktionen y = 2x + 1. Koefficienten 2 vid x avslöjar hur brant grafen ska ritas. Termen 1 berättar var grafen skär y-axeln. Riktningskoefficienten beräknas genom att förändringen på y-axeln divideras med förändringen på x-axeln. Tecknet "Delta" låter man ofta beteckna förändring av ett bestämt värde. |
y ökar från +3 till +7, d.v.s. 7 - 3 = 4 enheter, medan x ökar från +1 till +3, d.v.s. 3 - 1 = 2 enheter. Rikningskoefficienten för grafen är 2, koefficienten vid x. Man kan också beräkna riktningskoefficienten genom att rita en rätvinklig triangel vid linjen och beräkna förändringen på y-axeln och dividera med förändringen på x-axeln.
Gör nu test 2 i Ekvationssystemet.