© feb. 2000 Hugo och Tomas Rasmus

Bråk multiplikation och division 

Introduktion 1.

Förkortning och förenkling av bråk.

Vi repeterar faktorisering, titta på fenonemet med faktorer. 

Ta till exempel: 

D.v.s. talet 6 har multiplikationsfaktorerna 2 och 3. Alla hela tal har multiplikationsfaktorer, två eller fler, utom primtalen.

Exempel: 2, 3, 5, 7, 11, 13, 17, 19, 23 ...o.s.v. 

Ibland förekommer uppgifter med bara bokstäver, men även då kan man
faktorisera.

Ett exempel:     

Talet 1 har ingen betydelse för multiplikation, därför används det aldrig som en faktor.

Kom ihåg att ett bråkstreck betyder alltid division.

Vi tittar på några exempel på hur man kan använda gemensamma multiplikationsfaktorer för att förkorta bråk

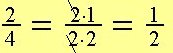
  Vi ser att:

och

Den gemensamma faktorn är 2. Vi förkortar bråket med 2.

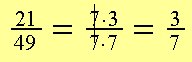
   Vi ser att:

och

Den gemensamma faktorn är 7. Vi förkortar bråket med 7.

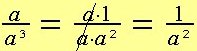
  Vi ser att:

och

Värdet a är den gemensamma faktorn, vi förkortar bråket med a.

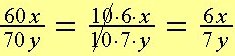
  Vi ser att:

och

Den gemensamma faktorn är 10, vi förkortar bråket med 10.

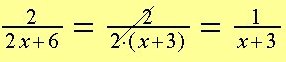
Faktorisera först (2X + 6) = 2(x + 3)

Den gemensamma faktorn är 2, vi förkortar bråket med 2.

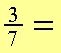
Primtal har bara två multiplikationsfaktorer, det egna talet och 1. Eftersom det inte finns några gemensamma faktorer går bråket inte att förkorta

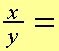
Olika variabler har även de bara multiplikationsfaktorerna sig själv och 1. Då inga gemensamma faktorer finns är det omöjligt att förkorta.

Gör nu test 1 i Multiplikation och divition av bråk.