© jan. 2000 Hugo och Tomas Rasmus

Faktorisering

Introduktion 1.

Du måste kunna avsnitt 4, (förenkla binom), för att klara av faktorisering.

Titta på fenomenet med faktorer.

Ett exempel:   

eller

D.v.s. talet 10 har multiplikationsfaktorna 5 och 2.  

Alla hela tal har två eller flera multiplikationsfaktorer, förutom de tal som kallas primtal, som exempelvis: (2, 3, 5, 7, 11, 13, 17, 19, 23 ... o.s.v. )

Vi tar ett multiplikationsexempel med bokstäver och tal:     

Uttrycket 3x+6  har två termer, därför att +  delar uttrycket.

3x  har två faktorer: 3 och x. 

Talet 6 har två faktorer:   och  d.v.s. faktorna 3 och 2.

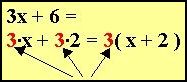
Talet 3 är en faktor i de båda termerna. Vi kan se att talet 3 tillhör de båda faktorerna i uttrycket 3x+6, d.v.s. det kan faktoriseras eller med andra ord: man kan ta 3 utanför parentes och uttrycket 3x+6 blir 3(x+2)

Bryt den största gemensamma faktorn och sätt denna utanför parentesen.

Exempel	Faktorer
	och
	och
	och

Försök nu med test nr.1 i faktorisering.