Rasmus.is - Faktorisering av uttryck

Faktorisering av uttryck

Lektion 4 Faktorisering genom utredning

Vi repeterar hur två parenteser multipliceras ihop.

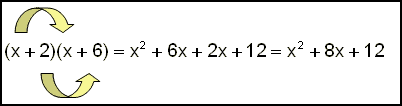Varje term i den ena parentesen multipliceras med varje term i den andra.

Om vi använder oss av bokstäver istället för nummer ser det ut på följande sätt:

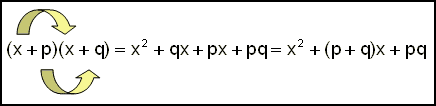Faktorisering innebär att man arbetar i motsatt riktning, dvs. att man sätter tillbaka termerna i deras två parenteser.

Vi behöver finna två heltal, p och q, så att när de multipliceras ihop så får vi 12 och när de adderas får vi 8.

Vi prövar några tal. Vi kallar det mindre talet för p och det större för q.

Detta är heltalen vi behöver överväga.

p∙q	p+q
1∙12 = 12	1+12 = 13
2∙6 = 12	2+6 = 8
3∙4 = 12	3+4 = 7

Det är lätt att se att när p = 2 och q = 6 så finner vi det vi söker.

Svaret är :

Exempel 1

Faktorisera x² − 7x + 12

I det här exemplet måste både p och q vara negativa. Vi vet det därför att de måste vara positiva när de multipliceras men negativa när de adderas ihop. När två negativa tal multipliceras ihop blir produkten positiv.

Om termen utan x är positiv och termen x är negativ så måste både p och q vara negativa

Talen vi behöver överväga visas i nedanstående tabell:

p∙q	p+q
(−1)∙(−12) = 12	−1−12 = −13
(−2)∙(−6) = 12	−2−6 = −8
(−3)∙(−4) = 12	−3−4 = −7

Värdena p = −3 och q = −4 passar vårt exempel.

Lösningen är därför:

Exempel2

Faktorisera x² + 4x − 12

I detta exempel måste p och q ha olika tecken därför att vi får ett negativt tal när de multipliceras ihop. Summan av dem är dock positiv vilket betyder att det större talet ( q ) måste vara positivt.

Om två tal som multipliceras ihop blir negativt så betyder det att det ena talet måste vara negativt och det andra positivt

Talen vi behöver överväga visas i denna tabell:

p∙q	p+q
(−1)∙(12) = −12	−1+12 = 11
(−2)∙(6) = −12	−2+6 = 4
(−3)∙(4) = −12	−3+4 = 1

Talen p = −2 och q = +6 passar in på våra förutsättningar.

Lösningen blir därför:

Exempel 3

Faktorisera x² − x − 12

I detta exempel måste p och q ha olika tecken. Summan av dem är negativ vilket betyder att det större talet ( q ) måste vara negativt.

Om multipeln är negativ så måste det ena talet vara negativt och det andra positivt ( + - )

Talen vi behöver överväga visas i denna tabell:

p∙q	p+q
1∙(−12) = −12	1−12 = −11
2∙(−6) = −12	2−6 = −4
3∙(−4) = −12	3−4 = −1

De korrekta talen är p = 3 och q = −4

Lösningen är därför:

Gör nu test nummer 4 i faktorisering. Om du får 80% eller mer rätt så fortsätter du med nästa lektion.