© 2009  Rasmus ehf    och Jóhann Ísak

Vektorer

Introduktion 4  

 Skalärprodukt och vinkelräta vektorer

Hur kan vi hitta vinkeln mellan två vektorer? Cosinussatsen verkar vara ett bra hjälpmedel eftersom vi kan räkna ut vinkeln mellan två närliggande sidor i en triangel (se introduktion 3 på trianglar). Vi kan skapa en triangel med två vektorer och och - (se introduktion 1 i vektorer), men låt oss titta närmare på detta i en bild.

Vi kan utan vidare se vad koordinaterna för vektorerna är men vi ska räkna med almänna koordinater:

Cosinussatsen är som följer:

    c² = a² + b² − 2∙b∙a∙cos C

Här representerar || sidan a i satsen, || sidan b, | - | sidan c och vinkeln C heter v° hos oss. Låt oss nu sätta in våra variabler i satsen.

| - |² = ||² + ||² - 2∙||∙ ||∙cos v°

Nu kan vi använda avståndsformeln för att hitta längden på vektorerna. Eftersom vi har potensen två på de termer där vi använder avståndsformeln så tar det ut kvadratroten.

    (x_a − x_b)² + (y_a − y_b)² = x_a² + y_a² + x_b² + y_b² − 2∙||∙ ||∙cos v° 

Om vi använder kvadreringsregeln på vänsterledet så ser det ut så här:

   x_a² − 2x_ax_b + x_b² + y_a² − 2y_ay_b + y_b²

Nu har vi alla termer i kvadrat på båda sidor om likhetstecknet. Efter att vi tagit ut dem så återstår denna ekvation:

   − 2x_ax_b − 2y_ay_b = − 2∙||∙ ||∙cos v° 

Om vi nu delar båda leden med −2 så får vi följande viktiga formel:

Leden på var sida om likhetstecknet kallas båda för skalärprodukt. Vi kan alltså räkna ut skalärprodukten på två sätt:

    Skalärprodukten mellan och = x_ax_b + y_ay_b  och  skalärprodukten mellan och = ||∙ ||∙cos v° 

Skalärprodukt kan även skrivas som multiplikation mellan två vektorer.
Dvs. på följande vis: ∙ = x_ax_b + y_ay_b  och  ∙ = ||∙ ||∙cos v° 

Exempel 1

Låt oss räkna ut skalärprodukten för vektorerna och på bilden här nedanför på de två sätt vi lärt oss.

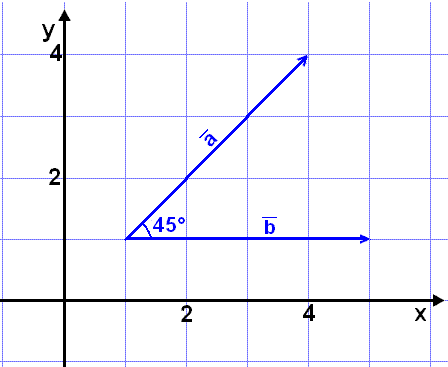
Vi kan läsa av koordinaterna för vektorerna och även längden på men längden på måste vi räkna ut.

Med koordinaterna:

Med vektorernas längder och cosinus av vinkeln mellan dem:

|| =

|| = 4

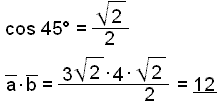
    x_ax_b + y_ay_b = ||∙ ||∙cos v° 

Om vi delar båda leden med ||∙| | får vi följande formel:

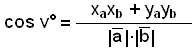Och om vi nu använder avståndsformeln för och så blir formeln som följer:

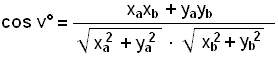Exempel 2

Låt oss räkna ut vinkeln mellan vektorerna

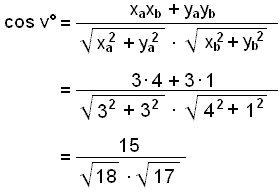
              ≈ 0,8575

           v° ≈ cos⁻¹ 0,8575 ≈ 31°

Exempel 3

Vilken vektor är lika lång som vektorn			och vinkelrät mot den?
Vi kallar denna vektor		och skriver upp skalärprodukten.

   x_ax_b + y_ay_b = ||∙ ||∙cos 90° 

Nu är cos 90° = 0 så vi får följande ekvation:

   x + 2y = 0

Vi har även ||²  = x² + y² = 5.

Vi löser dessa ekvationer tillsammans, x + 2y = 0 och x² + y² = 5.

    x = −2y  och x² = 5 − y²

   x² = 4y² = 5 − y²

 5y² = 5

   y² = 1

    y = ±1

Om y = 1 då är x = −2 och om y = −1 då är x = 2.

Vi har som sagt två möjligheter,

Vi ritar upp vektorerna.

Om vi generaliserar exemplet här ovanför så ser vi att vi kan rotera en vektor 90° genom att växla koordinaterna och byta tecken på en utav koordinaterna.

Regeln här ovanför gäller för lika långa vektorer eller om vi roterar samma vektor 90° åt höger eller vänster. Eftersom cos 90º = 0 så gäller följande regel för alla vektorer bortsett från deras längd:

Detta gäller även åt andra hållet.

Exempel  4

En triangel har hörnpunkterna A = (–3, –4), B = (17, –12) och  C = (5, 16). Låt oss räkna ut vinklarna.

Vi börjar med att hitta vektorer som representerar sidorna i triangeln.

Vi behöver inte räkna mera. Vektorerna och är uppenbarligen vinkelräta mot varandra och dessutom lika långa. Triangeln är rätvinklig og likbent så vinkeln A är 90º, B = 45º och C = 45º.

Exempel 5

En triangel har hörnpunkterna A = (–3, –3), B = (21, 7) och  C = (4, 14).

a)  Låt oss räkna ut vinkeln A.

Vi börjar med att räkna ut vektorerna och .

Sedan räknar vi ut längden på dem.

Nu kan vi räkna ut vinkeln mellan och .

Här multiplicerar vi med 2 både över och under strecket.

b)  Låt oss räkna ut höjden från C till sidan AB.

         sin A = h/||

         h = || · sin A

            = 13·2·2/₂

            = 13

c)   Låt oss räkna ut vektorn som representerar höjden från C till sidan AB.

Vektorn är vinkelrät mot och dessutom dubbelt så lång. Vi kan därför hitta vektorn  genom att rotera 90º och dela koordinaterna med 2.

Öva på dessa exempel och gör sedan test 4 i vektorer.

Obs! Kom ihåg att fylla i din checklista under tiden.