© 2009  Rasmus ehf    och Jóhann Ísak

Vektorer

Introduktion 3 

Vektorer i koordinatsystem

Exempel 1

Vi tänker oss att punkten A har koordinaterna (2, 2) och punkten B har koordinaterna (6, 5) (se bild). Koordinaterna för vektorn är:

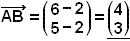
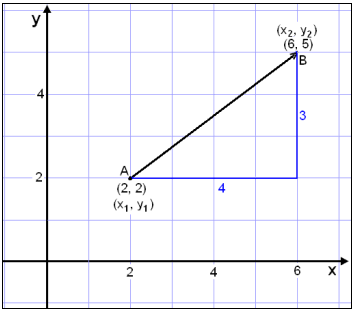
Vi kan använda avståndsformeln för att räkna ut avståndet mellan A och B och därmed vektorn ´s längd (Se Pythagoras sats, introduktion 2). Satsen är som följer:

Sätt in koordinaterna i formeln:

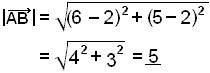
Som vi ser så får vi vektorns koordinater under rottecknet. Detta är ingen tillfällighet då längden på vektorn är lika lång som hypotenusan på den rätvinkliga triangel som vi ser på bilden.

Formeln för en vektors längd är som följer om vektorn börjar i punkten A = (x₁, y₁) och slutar i punkten B = (x₂, y₂). 

Om vi känner till koordinaterna för vektorn

då gäller följande formel:

Exempel 2

men bara hälften så lång (se bild).

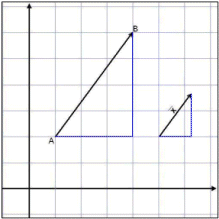
Trianglarna på bilden är likformiga så || = t∙||. Talet t måste vara förhållandet mellan trianglarnas sidor eller   = . Vi kan därför hitta koordinaterna på följande sätt:

Om vektorerna och är parallella då gäller följande formel:

= t∙

Exempel 3

Är vektorerna   och parallella?

Om vektorerna är parallella så finns ett tal t så att ekvationen = t∙ håller och ett annat tal r så att ekvationen = r∙ också håller. Vi kan räkna ut talen t och r med hjälp av x-koordinaterna och kontrollera om ekvationen även håller för y-koordinaterna.

= t∙

   3 = t∙13½ ger t = ³/13½ =²/9

   4 = t∙18 ger också t = ⁴/18 = ²/9

Vektorerna och är parallella.

= r∙

  3 = r∙6 ger r = ½

  4 = r∙9 ger däremot r = ⁴/9

Vektorerna och är inte parallella (och då är och inte heller parallella).

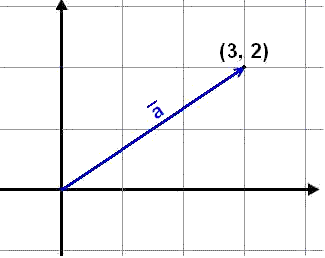
Vektorn på bilden här ovanför har koordinaterna . Begynnelsepunkten är (0, 0) och ändpunkten (3, 2) så vektorn har uppenbarligen samma koordinater som ändpunkten och det gäller för alla vektorer som börjar i origo eller punkten (0, 0).

Varje punkt i ett koordinatsystem kan representeras av en ortsvektor eftersom koordinaterna för punkten och ortsvektorn är de samma. Detta kan vara användbart när vi flyttar runt någonting i ett koordinatsystem.

Exempel 4

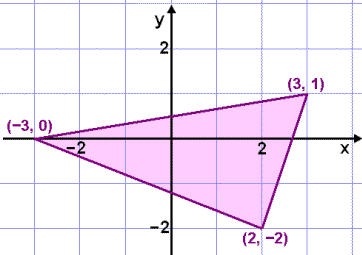
På bilden här ovanför ser vi en triangel som vi ska translatera (förflytta) med vektorn .

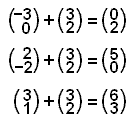
Vi har nu ortsvektorerna för dem nya hörnpunkterna. Bilden här nedanför visar translationen.

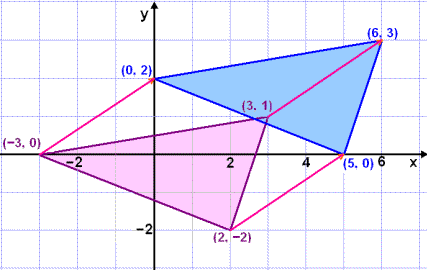
Exempel 5

Nu ska vi använda ortsvektorer för att hitta mittpunkten på linjen AB om A = (1, 2) och B = (4, 3).

Vi kallar koordinatsystemets mittpunkt för O (vilket är tradition) och mittpunkten på AB kallar vi M. Då gäller följande ekvation:

    = + ½∙

Vektorn är ortsvektorn för punkten M och har samma koordinater som den mittpunkt vi letar efter. Vektorn är ortsvektorn för punkten A och vi måste lägga till en halv vektor . Rita en bild för att visualisera vektorerna. Räkna med vektorernas koordinater.

Först hittar vi koordinaterna för vektorn .

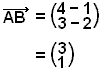
Räkna sedan ut .

    = + ½∙

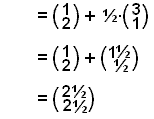
Koordinaterna för punkten M är de samma som för ortsvektorn eller (2½, 2½).

Vi kan göra det lättare för oss genom att skapa en formel för att räkna ut mittpunkten för vilken linje AB som helst.

2 = + ½∙ + - ½∙

Vi kan säga att ortsvektorn för mittpunkten på en linje är ett medeltal av ortsvektorerna för ändpunkterna på linjen. Om vi räknar med koordinaterna så ser vi att vi räknar ut medeltalet av x-koordinaterna å ena sidan och y-koordinaterna å andra sidan. Därmed har vi hittat en formel för att räkna ut mittpunkten, en mittpunktsregel.

Exempel 6

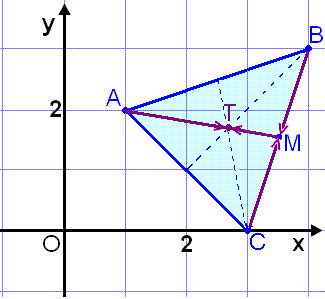
En triangel har hörnpunkterna A = (1, 2), B = (4, 3) och C = (3, 0). Låt oss räkna ut längden på den linje som går från vinkeln A till mittpunkten på linjen BC (kallas för median).

Först räknar vi ut mittpunkten på linjen BC med formeln här ovanför.

Vi kallar mittpunkten för M och räknar ut dess ortsvektor (se bild)

= ½∙ + ½∙

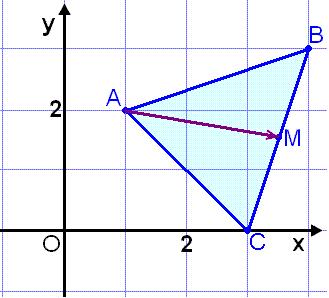Mittpunkten på linjen BC har som sagt koordinaterna M = (3½, 1½).

Nu räknar vi ut koordinaterna för vektorn .

Nu kan vi räkna ut längden på vektorn som representerar medianen.

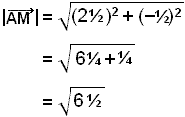
           ≈ 2,55

Skärningspunkten för de tre medianerna i en triangel ger oss koordinaten för triangelns tyngdpunkt (se punkten T på bilden). Vi kan hitta formeln för att räkna ut koordinaterna för T på liknande sätt som vi hittade mittpunktsregeln. Vi använder ortsvektorerna för triangelns hörnpunkter för att komma åt punkten T och lägger sedan ihop ekvationerna.

I introduktion 2 på trianglar lärde vi oss att en triangels medianer skär varandra i en punkt och delar varandra i förhållandet 2/1. Det betyder att vektorn är dubbelt så stor som så  
= ∙ och = −∙. Vi kan därför ställa upp förljande tre ekvationer:

= + ∙ 

= + ½∙ - ∙

= - ½∙ - ∙

När vi lägger ihop dessa ekvationer får vi följande ekvation:

3 = + +

När vi räknar ut koordinaterna för T så räknar vi ut medeltalet på x-koordinaterna och y-koordinaterna var för sig.

Vi kan med andra ord hitta skärningspunkten för medianerna eller tyngdpunkten T genom att räkna ut en sorts medeltal av ortsvektorerna för hörnpunkterna. Denna formel är en utvidgning på medelpunktsregeln.

Om vi hade visat att detta gäller ut från de tre hörnpunkterna då hade vi bevisat att medianerna måste skära varandra i en punkt och även regeln om att medianerna skär varandra på sådant vis att förhållandet på längderna är ²/1.

Exempel 7

Låt oss räkna ut tyngdpunkten T (skärningspunkten för medianerna) på triangeln som har hörnpunkterna A = (1, 2), B = (4, 3) och C = (3, 0) (se bild).

Tyngdpunkten är T = (2, 1).

Öva på dessa exempel och gör sedan test 3 i vektorer.

Obs! Kom ihåg att fylla i din checklista under tiden.