© 2008 Rasmus ehf og Jóhann Ísak
|
© 2008 Rasmus ehf og Jóhann Ísak |
Trigonometriregler |
|
Ekvationer av typen a sin x + b cos x = c
Diagrammet visar grafen till f(x) = sin x + 2 cos x.
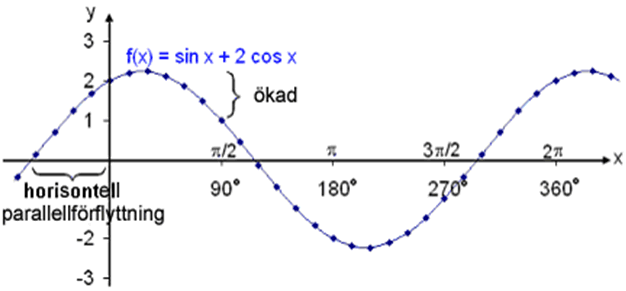
Häpnadsväckande nog ser det ut som en ordinär sinusvåg som har blivit förflyttad
med en amplitud som är större än den från basvågen. Vi har sett förut vad som
påverkar amplituden och hur amplituden kan ökas från värdet 1 genom att
multipliceras med en konstant som är större än 1. ( se trigonometrifunktioner
lektion 3). Vi har också sett att grafen till basfunktionen kan förflyttas
horisontellt genom att lägga till en konstant till vinkeln. Med detta i åtanke
borde vi kunna skriva om vår ekvation i formen
m sin (x + v), så att
m sin (x + v) = sin x + 2 cos x
Titta nu på grafen till g(x) =
sin x − 2 cos x.

Detta är uppenbart samma kurva förutom faktumet att förflyttningen nu är i motsatt riktning mot föregående, dvs. förflyttas till höger med samma längd som föregående kurva förflyttades till vänster. I detta fall borde vi kunna utforma den likvärdiga ekvationen.
m sin (x − v) = sin x − 2 cos x
Vi skriver nu om dessa uttryck genom att använda additionsteoremet:
sin (x + v) = sin x cos v + cos x sin v
sin (x − v) = sin x cos v − cos x sin v
Genom att multiplicera med m får vi:
m sin (x + v) = m sin x cos v + m cos x sin v
m sin (x − v) = m sin x cos v − m cos x sin v
Jämför resultaten med den originella ekvationen.
m sin (x + v) = 1 sin x + 2 cos x
= m cos v sin x + m sin v cos x
m sin (x − v) = 1 sin x − 2 cos x
= m cos v sin x − m sin v cos x
Vi ser att i båda fallen så måste följande vara sant:
m cos v = 1
m sin v = 2
Om vi dividerar den lägre ekvationen med den övre får vi följande:
tan v = 2/1
Vilket ger vinkeln v = tan−1 (2) ≈ 63,4°.
Við skulum nú teikna upp rétthyrndan þríhyrning með skammhliðarnar 1 og 2 eins og stuðlarnir eru í jöfnunni.
Om vi ritar en rätvinklig triangel med de kortare sidorna 1 och 2, samma värden som är i ekvationen, så kan vi beräkna längden på hypotenusan och se att:

cos
v = 1/![]() och
sin v = 2/
och
sin v = 2/![]() .
.
Genom att använda ekvationerna
m cos v = 1
m sin v = 2.
Ger oss att:
m∙1/![]() = 1
= 1
m =
![]()
Med andra ord kan vi skriva om ekvationen som:
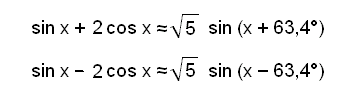
Vi ser att
amplituden av vågen i funktionerna f(x) = sin
x + 2 cos x och g(x) = sin x − 2 cos x
är ![]() .
.
Genom att generalisera och använda a och b för konstanterna får vi följande regel:
|
|
Vinkeln v kan hittas genom att använda:
|
tan v = b/a þar sem a > 0, b > 0 og 0° < v° < 90° |
Finn amplituden av funktionen f(x) = 3 sin x + 4 cos x.
Vi börjar med att skriva om funktionen.

Amplituden är 5.
Grafen av funktionen f(x) = 3 sin x + 4 cos x är en sinusvåg som har parallellförflyttats. Räkna ut med hur många grader och i vilken riktning vågen har parallellförflyttats.
f(x) = 3 sin x + 4 cos x
= 5 sin (x + v)
v = tan −1 (4/3) ≈ 53,1°
Vågen har parallellförflyttats med 53.1° åt vänster
(f(x) ≈ 5 sin (x + 53.1°).
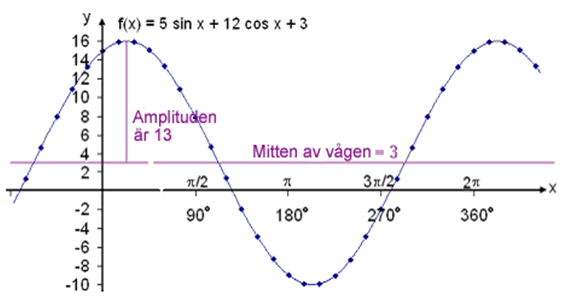
Given funktionen f(x) = 5 sin x + 12 cos x + 3. Finn amplituden, den maximalla höjden och parallellförflyttningen på vågen.
Skriv om f(x).
tan −1 (12/5) ≈ 67,4°
![]()
f(x) = 13 sin (x + 67,4°) + 3
Amplituden är 13 så den maximala höjden är 13 + 3 = 16. Titta på grafen.
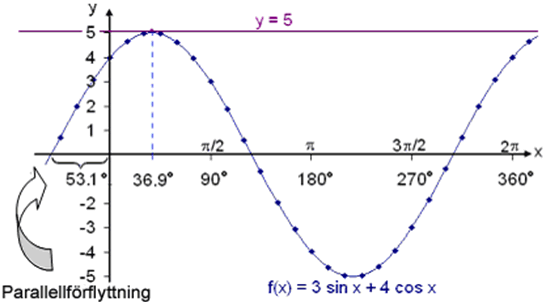
Lös
ekvationen 3 sin x + 4 cos x = 5 på intervallet 0° ![]() x <
360°.
x <
360°.
3 sin x + 4 cos x = 5
= 5 sin (x + 53,1°)
sin (x + 53,1°) = 5/5 = 1
x + 53,1° = sin −1 1 = 90° + k∙360°
x = −53,1° + 90° + k∙360°
x = 36,9°
Detta ger en lösning 36.9° i den första kvadranten.Det är intressant att titta på grafen. Vi ser att det inte finns någon annan lösning på det efterfrågande intervallet.
Finn alla
lösningarna till ekvationen sin x − ![]() cos x = 1.
cos x = 1.

Vi ser att
tan v =
![]() och v = tan (
och v = tan (![]() ) −1 =
) −1 =
![]() /3 (60°).
/3 (60°).
sin (x −
![]() /3) = ½
/3) = ½
|
(x −
|
|
x =
![]() /3 +
/3 +
![]() /6 + k∙2
/6 + k∙2![]()
=
![]() /2 + k∙2
/2 + k∙2![]()
Eller en andra möjlighet
(x −
![]() /3) =
/3) =
![]() −
−
![]() /6 + k∙2
/6 + k∙2![]()
x =
![]() /3 +
/3 +
![]() −
−
![]() /6 + k∙2
/6 + k∙2![]()
|
x = 7 |
7 |
Prova Test 3 på Trigonometriregler.
Kom ihåg att använda checklistan för att hålla ordning på ditt arbete.