© 2008  Rasmus ehf    og Jóhann Ísak

Trigonometriregler

Lektion 1

Pytagoras sats för Cosinus and Sinus

Matematik har många regler som hjälper oss  att förenkla och därigenom lösa de komplicerade trigonometriska funktionerna

Vi ska nu hitta och använda en av dem, förmodligen den mest användbara av dem alla.

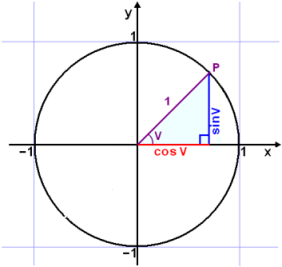
Denna regel kallas ofta för Pytagoras sats för sinus och cosinus. Diagrammet  visar en rätvinklig triangel ritad i enhetscirkeln. Pytagoras sats är sann för alla punkter  P på enhetscirkeln.

Detta innebär att
(sin v)2+(cosv)2=1. 

Denna regel skrivs vanligtvis i formen:

sin 2 v + cos 2 v = 1

Den kan skrivas på två sätt:

sin 2 v = 1 − cos 2 v

och

cos 2 v = 1 - sin 2 v

Exempel 1

Finn sin x om cos x = ⅓ och 0 x < /2 (x är en vinkel mellan 0° och 90°).

Vi kan lösa detta problem genom att använda en räknare,
cos −1 (⅓) ≈ 70.53° och därför är sin 70.53° ≈ 0.94. Om vi vill ha ett exakt svar kan vi göra detta exempel utan en räknare, genom att använda Pytgoras sats.


 

 

 

 

 

 

 

 

 

Exempel 2

Använd regeln  sin 2 v + cos 2 v = 1 för att hitta andra sätt att skriva uttrycket 1/ cos 2 v.

Ett sätt är genom att flytta sin 2 v över likhetstecknet, så att vi får cos 2 v = 1 − sin 2 v och sedan invertera båda sidorna av ekvationen. Detta ger oss

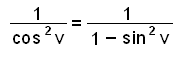
Det finns ett annat, inte uppenbart sätt, som leder till ett uttryck som kan vara väldigt användbart. Titta vad som sker om vi dividerar den originella ekvationen,  sin 2 v + cos 2 v = 1, med cos 2 v.

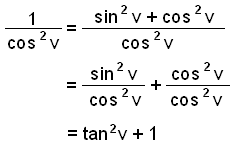
Vi har nu bevisat regeln:

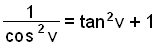
Exempel 3

Vi ska nu använda Pytagoras sats för trigonometriska funktioner för att hitta värdet på, först sin 2 v och sedan cos 2 v, givet sin 2 v = cos 2 v.
 

Först byter vi ut cos 2 v genom att använda regeln cos 2 v = 1 − sin 2 v.

      sin2 v = cos2 v

      sin2 v = 1 − sin2 v

   2∙sin2 v = 1

      sin2 v = ½

Nu byter vi ut sin 2 v genom att använda sin2 v = 1 − cos2 v.

          sin2 v = cos2 v

  1 − cos2 v = cos2 v

                 1 = 2∙cos2 v

         cos2 v = ½

Exempel 4

Lös ekvationen  cos2 x = sin x + 1

Byt först ut cos 2 x.

        cos2 x = sin x + 1

   1 − sin2 x = sin x + 1

                0 = sin2 x + sin x = sin x (sin x + 1)

Detta leder till  sin x = 0 or sin x = −1,

så att x = k∙ (k∙180°) eða x = 3/2 + k∙2 (270° + k∙360°).

Exempel 5

Förenkla ekvationen  

Här använder vi regeln som

(a + b)(a − b) = a2 − b2 och skriv sedan om  tan  x som í sin/cos  innan förenkling

Prova Test 1 på Trigonometriregler.

 Kom ihåg att använda checklistan för att hålla ordning på ditt arbete.