© 2008 Rasmus ehf og Jóhann Ísak
|
© 2008 Rasmus ehf og Jóhann Ísak |
Trianglar |
|
Sinus- och Cosinusreglerna
Under lektion 2 introducerades vi till regeln
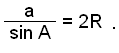
Denna regel gäller också om vi använder
vinklarna B och C och sidorna b eller c istället för vinkeln A och sidan a.
Detta leder till följande regel kallad sinussatsen:
|
|
Vi använder denna regel för att hitta okända vinklar och sidor i en triangel när vi vet vad en vinkel är och den motsatta sidan till den vinkeln tillsammans med antingen en annan sida eller vinkel.
Detta är basregeln vilken används i mätning av land och karttillverkning. Vi kan skriva om regeln i tre delar att använda beroende på sidorna och vinklarna som är kända.
|
|
|
|
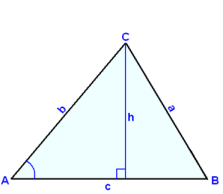
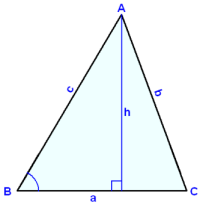
Följande diagram visar samma triangel stående i tur på varje av de tre sidorna. Vi kan skriva en formel för arean i varje fall genom att använda olika baser och höjder.
 |
 |
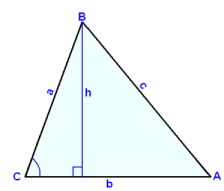 |
F = ½∙c∙h F = ½∙a∙h F = ½∙b∙h
Genom att använda regeln x = motsatt sida/hypotenusa så får vi
sin A = h/b sin B = h/c sin C = h/a
h = b∙sin A h = c∙sin B h = a∙sin C
Triangelns area är därför:
|
F = ½ ∙c∙b∙sin A F = ½∙a∙c∙sin B F = ½∙b∙a∙sin C |
Arean F är så klart samma i alla fallen och vi kan använda dessa formler till att skriva sinussatsen på ett annat sätt. Vi kan dividera alla genom ½∙a∙b∙c.
½∙b∙c∙sin A = ½∙a∙c∙sin B = ½∙a∙b∙sin C = F
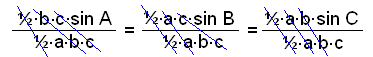
Vilket leder till sinussatsen skriven som:
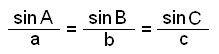 |
I en spetsvinklig triangel så är sidan a = 12 cm, sidan c = 13 cm och vinkeln A = 60°. Finn vinkeln C, sidan b och arean på triangeln.
Först ritar vi och märker ett diagram.
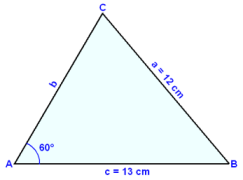
Sedan använder vi sinussatsen för att finna vinkeln C.
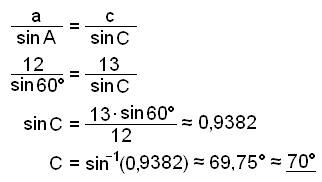
B ≈ 180° − 69,75° − 60° ≈ 50,25° ≈ 50°
Sedan använder vi regeln för att finna sidan b.
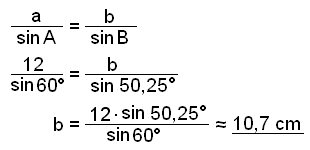
Slutligen använder vi regeln för arean för att finna arean F.
F = ½∙b∙c∙sin A ≈ ½∙10,7∙13∙sin 60° ≈ 60 cm2
I en trubbigt vinklad tringel så är sidan a = 12 cm, sidan c = 13 cm and vinkeln A = 60°. Finn vinkeln C, sidan b och arean till triangeln.
Detta är samma exempel som ovan förutom att en vinkel i triangeln är trubbig ( större än 90°).
När vi fann vinkeln C i exempel1 ovan så antog vi att räknaren gav oss det rätta svaret. Beräkningarna var som följer:
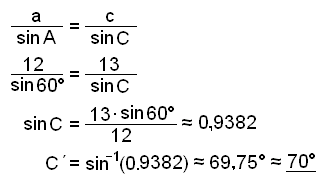 |
sinC = 0,9382 |
Vi får redan på att denna triangel har en trubbig vinkel så vi måste komma ihåg regeln som ger oss den andra lösningen till ekvationen. Denna regel är:
sin v° = sin (180° − v°)
Detta ger oss den
trubbiga vinkeln
C ≈ 180° − 70°
≈ 110°
och
därför är vinkeln
B ≈ 180° − 60° −
110° ≈ 10°
Men hur kan vi förklara att det kan vara två olika trianglar med de givna måtten? Titta på diagrammet.
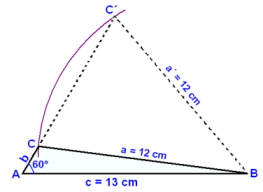
Först ritar vi baslinjen c = 13 cm. Sedan ritar vi en vinkel på 60°i ena änden av baslinjen och märker den A. Märk den andra sidan av baslinjen B. Genom att använda B som center, ritar vi en cirkel med radien 12 cm. Denna cirkel skär armen till vinkeln A på två ställen vilket säger oss att det finns två möjliga lösningar för punkten C. En leder till en spetsvinklig -, och den andra till en trubbigt vinklad triangel ( se diagrammet).
Vi fortsätter nu med exempel 2 och finner sidan b.
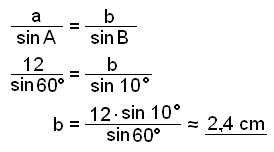
Slutligen beräknar vi arean på triangeln.
F = ½∙b∙c∙sin A ≈ ½∙2,4∙13∙sin 60° ≈ 13,5 cm2
I en trubbigt vinklad triangel så är sidan a = 15 cm, side c = 6 cm och vinkeln A = 60°. Finn vinkeln C och sidan b.
Rita och märk en triangel.
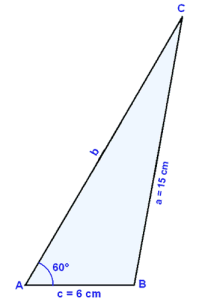
Använd sinussatsen.
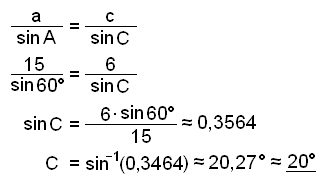
B ≈ 180° − 60° − 20,27° ≈ 99,73° ≈ 100°
Finn sidan b.
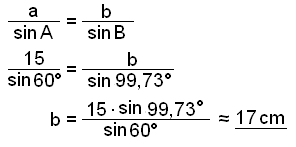
Dessa beräkningar överensstämmer med diagrammet. Det finns ingen annan triangel som uppfyller de givna måtten.
Från exemplet ovan kan vi dra följande slutsatser:
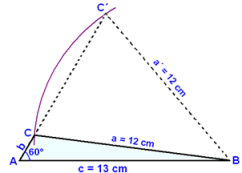
|
När den sidan motsatt till den givna vinkeln är kortare än den närliggande sidan till vinkeln (baslinjen) så måste vi veta om triangeln är spetsig eller trubbig. Om vi inte har denna extra information så finns det två typer av trianglar och därför två olika lösningar. |
I triangeln ABC, är sidan c = 12 cm, vinkeln A = 60° och vinkeln B = 80°. Finn sidorna b och c.
Rita ett diagram med c = 12 cm som baslinje. Vi kan lätt finna den tredje vinkeln i denna triangel och om vi vet alla vinklarna så finns det bara en möjlig lösning.
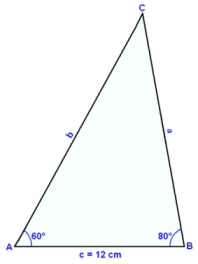
Först måste vi finna vinkeln C.
C = 180° − 60° − 80° = 40°
Nu använder vi sinussatsen för att finna sidan a.
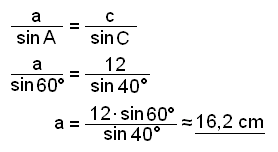
Slutligen finner vi sidan b.
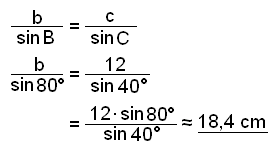
Vi kan alltid använda sinussatsen för att
finna okända sidor och vinklar i en triangel om vi vet en sida och två vinklar.
(se exempel 4).
vi kan också använda sinussatsen till om vi vet två sidor och vinkeln motsatt en
av sidorna (se exemplen 1-3). I detta fall måste vi veta om triangeln är
spetsigvinklig eller trubbigt vinklad.
Men hur är det då med trianglar där vi vet
två sidor och vinkeln mellan dem, eller endast tre sidor och inga vinklar?
Vi kan enkelt rita en triangel om vi får denna information och därför bör det
vara möjligt att beräkna de okända vinklarna och sidorna. Sinussatsen fungerar
inte så vi måste finna någon annan metod.
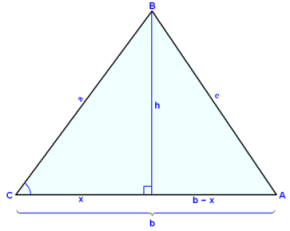
Vi ritar och märker en triangel ABC och delar den i två rätvinkliga trianglar genom att rita in höjden h. Nu använder vi Pytagoras sats i båda dessa trianglar.
h2 = a2 − x2 og h2 = c2 − (b − x)2 = c2 − b2 + 2∙b∙x − x2
Genom att beräkna dessa två ekvationer får vi
c2 − b2
+ 2∙b∙x − x2 = a2 − x2
Lös denna ekvation för c2.
c2 = a2 + b2 − 2∙b∙x
Nu gör vi oss av med
x
i formeln genom att använda regeln
cos C = x/a vilket ger oss
x = a cos C.
Genom
att sätta in detta i formeln istället för x ger det följande formel:
|
c2 = a2 + b2 − 2∙b∙a∙cos |
Denna formel kallas cosinusteoremet och kan användas till att finna sidan c om vi kan sidorna a och b och vinkeln dem emellan, vinkeln C (se diagrammet ovan).
Det kan bevisas att cosinusteoremet även gäller för trubbigt vinkade trianglar. Beviset är väldigt likt det bevis som finns för spetsvinkiga trianglar.
Om vi använder andra vinklar och sidor så får vi följande motsvarande formler:
|
a2 = b2 + c2 − 2∙b∙c∙cos A b2 = a2 + c2 − 2∙a∙c∙cos B |
Om alla sidor i en triangel är kända så kan vi använda cosinusteoremet till att finna vinklarna. T.ex. om vi vill finna vinkeln C så löser vi formeln för cos C och använder sedan räknarna till att finna vinkeln.
c2 = a2 + b2 − 2∙b∙a∙cos C
2∙b∙a∙cos C = a2 + b2 − c2
Genom att dividera med 2ab får vi följande:
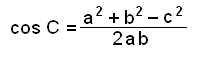 |
Motsvarande formel för de andra vinklarna är:
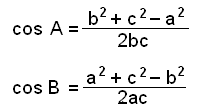 |
I triangeln ABC är sidan c = 12 cm och b = 15 cm. Vinkeln A som ligger mellan sidorna b och c är 60°. Finn sidan a, vinkeln C och arean till triangeln.
Först ritar vi och märker ett diagram.
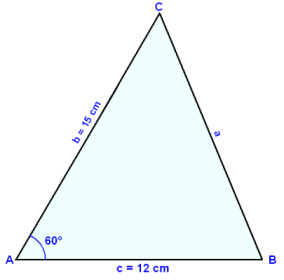
Genom att använda cosinusteoremet för cos A.
a2 = b2 + c2 − 2∙b∙c∙cos A
= 152 + 122 − 2∙15∙12∙cos 60°
= 225 + 144 − 180 = 189
![]()
Nu kan vi antingen använda sinussatsen eller cosinusteoremet till att finna Vinkeln C. Vi kommer använda sinussatsen.
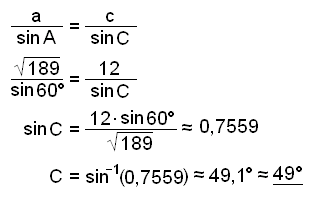
Slutligen finner vi arean.
F = ½∙b∙c∙sin A ≈ ½∙15∙12∙sin 60° ≈ 78 cm2
I triangeln ABC, så är a = 12 cm, b = 11 cm och c = 13 cm. Finn triangelns area.
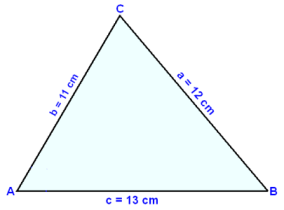
Innan vi kan finna arean behöver vi finna en vinkel. Vi kommer använda cosinusteoremet till att finna vinkeln C.
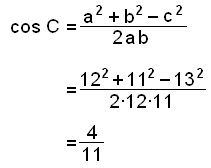 |
| C = cos-1(4/11) |
| C ≈ 68,7° |
Nu kan vi finna triangelns area.
F = ½∙a∙b∙sin
C ≈ ½∙12∙11∙ sin 68,7° ≈ 61,5 cm2
Prova test 3 på trianglar.
Kom ihåg att använda checklistan för att hålla ordning på ditt arbete.