© 2008 Rasmus ehf og Jóhann Ísak
© 2008 Rasmus ehf og Jóhann Ísak |
Trianglar |
|
Regler för trianglar
Det är ett allmänt tillvägagångssätt att märka hörnorna på en triangel med stora bokstäver och sidorna med små bokstäver.
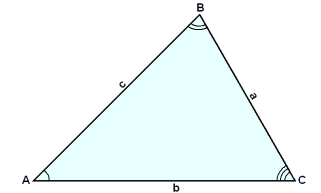
Det är även allmänt tillvägagångssätt att märka sidan som är motsatt till vinkeln A med ett litet a, sidan motsatt vinkeln B med ett litet b och sidan motsatt vinkeln C med ett litet c (se diagrammet).
Sidorna som formar armarna till vinkeln A kallas intilliggande till A. Sidan på vilken triangeln står kallas triangelns bas.
Summan av vinklarna i en triangel är 180° . Det kan enkelt ses genom att rita en rak linje genom vinkeln B och parallelt med sidan b (se diagrammet).
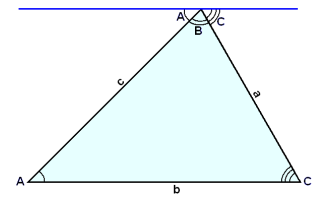
Vinklarna som formas med denna linje är lika
med A, B och C (genom regeln att omväxlande vinklar mellan parallella linjer är
lika).
Vidare A + B + C = 180° då de tillsammans utgör en rak linje.
Den raka linjen från vinkeln B som är vinkelrätt mot baslinjen kallas triangelns höjd. Höjden märks med h i diagrammet nedan.
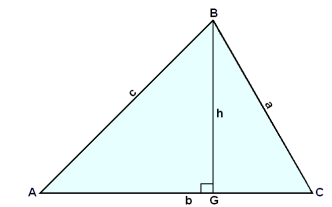
Du har tidigare lärt dig att triangelns area ges med formeln.
Area F = ½∙b∙h
Bokstaven G används här för att märka punkten där höjden och basen genomskär varandra. Denna punkt kallas ibland den vinkelrätta projektionen av punkt B på linje b.
Två trianglar sägs vara likformiga om alla vinklar i en av trianglarna är lika med alla vinklarna i den andra. Om vi vill visa att två trianglar är likformiga så räcker det att visa att två vinklar är lika. Om två vinklar är lika så är det uppenbart att den tredje vinkeln i varje av trianglarna måste vara lika.
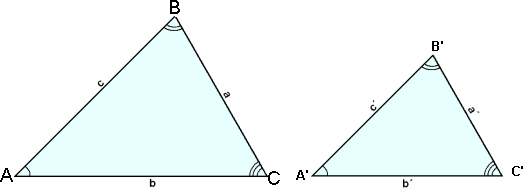
Trianglarna i diagrammet är likformiga. Det
gäller att förhållanden mellan motsvarande sidor överensstämmer.
Med andra ord:
| och |
Vi ska nu göra några exempel genom att använda dessa förhållanden.
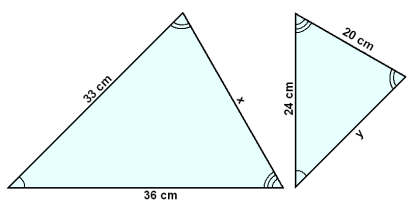
Trianglarna i diagrammet är likformiga med likadana vinklar märkta på samma sätt. Vi vill beräkna längderna på sidorna märkta med x och y.
Vi börjar med att märka trianglarna så att vi lättare kan se vilka sidor som överensstämmer med varandra.
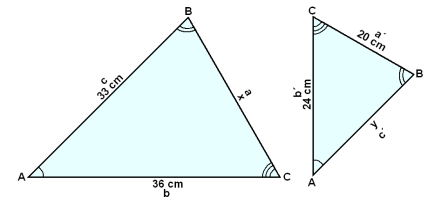
Vi kan skriva följande förhållanden:
b/c = 36/33 = 24/y = b´/c´
Detta betyder att y/24 = 33/36 och därför är y = 24∙33/36 = 22 cm.
Dessutom är a/b = x/36 = 20/24 = a´/b´
Vilket ger oss x = 36∙20/24 = 30 cm.
En annan regel för förhållanden i trianglar kan härledas.
 |
|
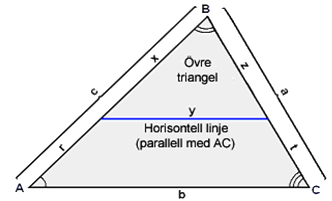
Vi ritar en rak linje som skär två sidor av triangeln och är parallell med den tredje sidan. Denna linje delar triangeln i två delar, den övre delen är en triangel som är likformig med ABC, den originella triangeln. Vi kommer att märka sidorna på den mindre triangeln med bokstäverna x, y och z. Följande är nu sant:
Linjen som vi har ritat delar sidan c i två delar, x och r och sidan a delas till z och t. När vi sätter in x + r istället för c och z + t istället för a i ekvationen ovan så får vi följande resultat:
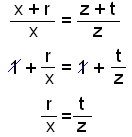
Vi har nu visat att en linje genom två sidor av en triangel som är parallell med den tredje sidan delar dessa två sidor i samma förhållande.
Två sidor av triangeln ABC, AB och BC har 30 cm i längd och den tredje sidan AC, baslinjen, är 42 cm. Vi ritar en linje genom en punkt X på AB parallellt med basen med en längd på 14 cm. Finn längden på linjerna BX och AX.
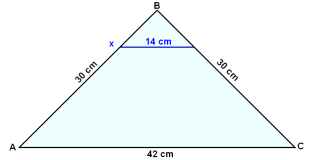
14/42 = XB/30
XB = 30∙14/42 = 10 cm
AX = 30 − 10 = 20 cm
I de flesta fall då vi vill finna storleken på vinklarna så måste vi antingen rita ett exakt diagram och mäta vinklarna eller använda trigonometrireglerna.
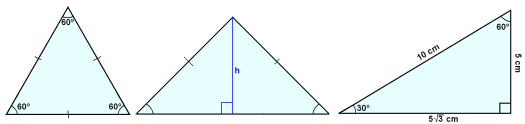
Liksidig. Likbent. Rätvinklig.
I en liksidig triangel är alla sidor lika och alla vinklar är 60°.
I en likbent triangel är två sidor av samma längd och två vinklar (vinklarna som formas av baslinjen) är likadana. Om vi vet en vinkel i en likbent triangel så kan vi hitta de andra vinklarna. Den vinkelrätta linjen från hörnet till baslinjen (höjden) i en likbent triangel delar triangeln i två likadana rätvinkliga trianglar.
Sidorna på en rätvinklig triangel ABC bekräftar Pythagoras sats, det är att a2 + b2 = c2.
Motsatsen är också sann. Om Pythagoras sats håller så är triangel rätvinklig.
Vi kan kontrollera om den tredje triangel i diagrammet ovan är rätvinklig genom att använda Pythagoras sats.
52 + (5![]() )2 = 102
)2 = 102
25 + 75 = 100
Lägg märke till längden på hypotenusan (10cm) i denna triangel är dubbelt så lång som den kortaste sidan (5cm).
När detta är fallet är alltid vinklarna i triangeln 30°, 60°och 90°.
Finn arean på en liksidig triangel med sidor av längden 10cm,
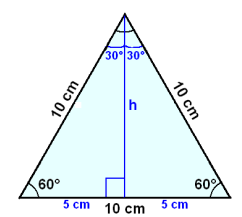
Vi börjar med att rita in höjden, h, på triangeln. Detta delar upp triangeln i två likadana rätvinkliga trianglar. Genom att använda Pythagoras sats kan vi beräkna h.
h2 + 52 = 102
h2 = 102 − 52 = 100 − 25 = 75 = 52∙3
h = 5![]() ≈ 8,7
≈ 8,7
Area A = ½∙10∙h ≈ ½∙10∙8,7 ≈ 43 cm2
Benen på en likbent triangel är 30 cm långa och baslinjen är 42 cm. Hitta längden på en linje som ritas genom de två likadana sidorna, parallellt med basen och 10 cm ovanför den.
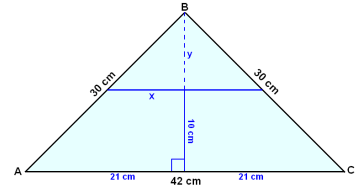
Först delar vi triangeln i två rätvinkliga trianglar genom att rita in höjden, h, från hörnet till basen. Nu kan vi använda Pythagoras sats till att beräkna höjden.
h2 + 212 = 302
h2 = 302 − 212 = 459
h ≈ 21,4
y = h − 10 ≈ 21,4 − 10 ≈ 11,4 cm
Genom att amvända förhållanderegeln för likformiga trianglar får vi:
y/h = x/ 21
x ≈ 21∙11,4/ 21,4 ≈ 11 cm
Därför är längden på den parallella linjen 22 cm.
Vi ska rita den rätvinkliga triangeln genom att använda hypotenusan AB som baslinje så att vinkeln i hörnet är 90°. Vi ritar sedan höjden från C ned på AB så som visas i diagrammet:
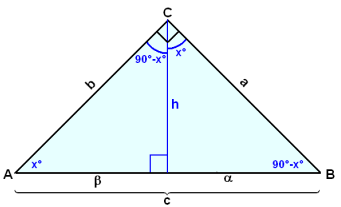
Denna linje delar vinkeln i hörnet i två delar (inte lika såvida inte triangeln är likbent). Om ena delen är x°, då måste den andra vara 90°− x°. Vi kan enkelt se att de två basvinklarna måste vara 90° − x° (på höger sida) och x° (på vänster sida) eftersom summan av vinklarna i alla trianglar är 180°.
Lägg märke till att alla vinklar i båda de mindre trianglarna och även i den originella triangeln ABC är lika, och är 90°, x° och 90° − x°. Dessa tre tringlar är därför likformiga.
Följande regler gäller för alla rätvinkliga trianglar:
Höjden ritad från ett hörn till hypotenusan delar in en rätvinklig triangel i två trianglar som båda är likformiga med den originella triangeln.
Detta ger upphov till tre uppsättningar förhållanden.
Genom att använda de grekiska bokstäverna a för den motsatta sidan till vinkeln märkt x° och b för den motsatta sidan till vinkeln märkt 90°− x° får vi följande:
De två mindre trianglarna är likformiga därför
![]()
Den originella triangeln och triangeln med den övre vinkeln x är likformiga därför
![]()
Den originella triangeln och triangeln med den övre vinkeln 90°−x° är likformiga därför
![]()
En rätvinklig triangel är given med de två kortare sidorna på längderna 7 cm och 10 cm. Höjden som ritas på hypotenusan delar triangeln i två trianglar. Finn arean på dessa två trianglar.
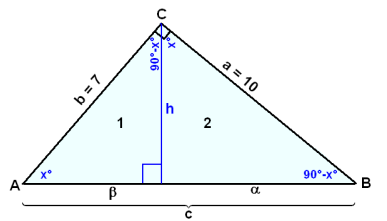
Först använder vi Pytagoras sats till att beräkna längden på hypotenusan c.
c2 = 102 + 72 = 149, þá er c ≈ 12,2 cm
Sedan använder vi ett av förhållandena ovan till att beräkna a.
a/c = a/a
a = a2/c ≈ 102/12,2 ≈ 8,2 cm
Och sedan b.
b ≈ 12,2 − 8,2 ≈ 4 cm
Nu måste vi beräkna höjden h .
b/c = h/a
h = ab/c ≈ 10∙7/12,2 ≈ 5,7 cm
Areorna hittas nu enkelt.
Area F1 = ½∙b∙h ≈ ½∙4∙5,7 ≈ 11,4 cm2
Area F2 = ½∙a∙h ≈ ½∙8,2∙5,7 ≈ 23,4 cm2
Prova test 1 på Trianglar.
Kom ihåg att använda checklistan för att hålla ordning på ditt arbete.