© 2008 Rasmus ehf och Jóhann Ísak
© 2008 Rasmus ehf och Jóhann Ísak |
Ekvationer III |
|
Tredje- och fjärdegradsekvationer
Hur kan vi lösa ekvationer såsom tredjegradsekvationen nedan?
x3 − x2 – 4x + 4 = 0
Det finns en extremt komplicerad formel för att lösa tredjegradsekvationer. Visa räknare har denna formel inbyggd och kan därför användas till att lösa tredjegradsekvationer.
Vi ska lära oss hur dessa ekvationer kan lösas genom att faktorisera. Om ekvationen har lösningar som är heltal a, b och c så kan vi faktorisera ekvationen som följer:
x3 − x2 – 4x + 4 = (x − a)(x − b)(x − c) = 0
När vi multiplicerar ihop parenteserna så ser vi att den konstanta termen, 4, måste vara talet som vi får när vi multiplicerar ihop a, b och c.
abc = 4
Alla lösningarna a, b och c måste vara faktorer av 4 så att det inte är många hela tal som vi måste överväga.
Vi har endast följande möjligheter.
±1, ±2 og ±4
Vi ska undersöka alla dessa tal för att hitta vilka som är lösningar till ekvationen.
f(1) = 13 − 12 – 4∙1 + 4 = 0 1 är en lösning
f(−1) = (−1)3 − (−1)2 – 4∙(−1) + 4 = 6
f(2) = 23 − 22 – 4∙2 + 4 = 0 2 är en lösning
f(−2) = (−2)3 − (−2)2 – 4∙(−2) + 4 = 0 −2 är en lösning
Vi har nu hittat tre lösningar så vi behöver inte pröva 4 eller −4 då tredjegradekvationer endast har max tre lösningar.
Dessa tre tal ger oss värdena av a, b och c och vi kan faktorisera ekvationen.
x3 − x2 – 4x + 4 = (x − 1)(x − 2)(x + 2) = 0
Denna metod involverar att hitta heltalen som är faktorer av (kan divideras till ) den konstanta termen och sedan testa huruvida dessa heltal är lösningar till ekvationen.
Dessvärre kan vi inte anta att lösningar till en tredjegradekvation är alla
heltal.
Men, om vi kan hitta en heltalslösning, låt oss säga att det är x = a då, enligt
restsatsen, vet vi att (x − a) är en faktor utav ekvationen. Vi kan hitta en
annan faktor, en andragradsfaktor, genom division. Då kan vi lösa
andragradsekvationen genom att använda formeln för att lösa dessa.
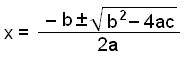
Exempel 1
Lös ekvationen x3 − 3x2 – 2x + 4 = 0
Vi sätter talen som är faktorer av 4 in i ekvationen för att se om någon av dem är korrekta.
f(1) = 13 − 3∙12 – 2∙1 + 4 = 0 1 är en lösning
f(−1) = (−1)3 − 3∙(−1)2 – 2∙(−1) + 4 = 2
f(2) = 23 − 3∙22 – 2∙2 + 4 = −4
f(−2) = (−2)3 − 3∙(−2)2 – 2∙(−2) + 4 = −12
f(4) = 43 − 3∙42 – 2∙4 + 4 = 12
f(−4) = (−4)3 − 3∙(−4)2 – 2∙(−4) + 4 = −100
Den enda heltalslösningen är x = 1. När vi har hittat en lösning behöver vi egentligen inte testa några andra tal för att vi kan nu lösa ekvationen genom att dividera med (x − 1) och försöka att lösa andragradsekvationen som vi får från divisionen.
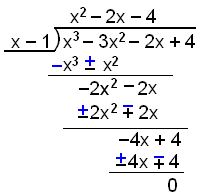
Nu kan vi faktorisera vårt uttryck som följer:
x3 − 3x2 – 2x + 4 = (x − 1)(x2 − 2x − 4) = 0
Nu återstår det för oss att lösa andragradsekvationen.
x2 − 2x − 4 = 0
Vi använder formeln för andragradsekvationer med a = 1, b = −2 och c = −4.
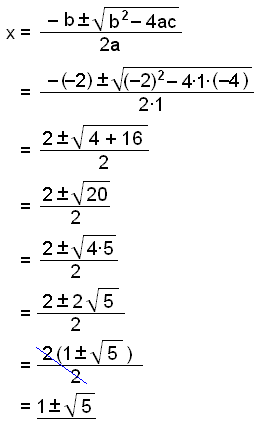
Vi har nu hittat alla tre lösningarna till ekvationen x3 − 3x2 – 2x + 4 = 0.
De är:
x = 1
x = 1 + ![]() 5
5
x = 1 − ![]() 5
5
Exempel 2
Vi kan enkelt använda samma metod för att lösa en fjärdegradsekvation eller en ekvation av en ännu högre grad. Lös ekvationen f(x) = x4 − x3 − 5x2 + 3x + 2 = 0.
Först hittar vi heltalsfaktorerna till den konstanta termen, 2.
Heltalsfaktorerna av 2 är ±1 och ±2.
f(1) = 14 − 13 − 5∙12 + 3∙1 + 2 = 0 1 är en lösning
f(−1) = (−1)4 − (−1)3 − 5∙(−1)2 + 3∙(−1) + 2 = −4
f(2) = 24 − 23 − 5∙22 + 3∙2 + 2 = −4
f(−2) = (−2)4 − (−2)3 − 5∙(−2)2 + 3∙(−2) + 2 = 0 vi har hittat en andra lösning.
De två lösningarna vi har hittat 1 and −2
innebär att vi kan dividera med x − 1 och x + 2 och det kommer inte att bli
någon rest. Vi gör detta i två steg.
Dividera först med x + 2
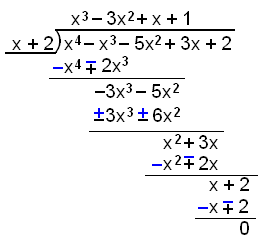
Dividera nu den resulterande tredjegradsfaktorn med x − 1.
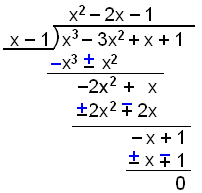
Vi har nu faktoriserat
f(x) = x4 − x3 − 5x2 + 3x + 2
f(x) = (x + 2)(x − 1)(x2 − 2x − 1) och nu återstår bara att lösa andragradekvationen.
x2 − 2x − 1 = 0. Vi använder formeln med a = 1, b = −2 och c = −1.
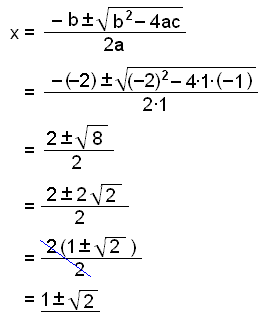
Nu har vi hittat totalt fyra lösningar. Dessa är:
x = 1
x = −2
x = 1 + ![]() 2
2
x = 1 − ![]() 2
2
Ibland kan vi lösa en tredjegradsekvation genom att sätta termerna två och två inom parentes och hitta en faktor som de har gemensamt. Låt oss titta på ett exempel på detta.
Exempel 3
Lös ekvationen x3 − 2x2 − 4x + 8 = 0
x3 − 2x2 − 4x + 8 = 0 (x3 − 2x2) − (4x − 8) = 0 [x2(x − 2) − 4(x − 2)] = 0 (x − 2)[x2 − 4] = 0 (x − 2)(x − 2)(x + 2) = 0 |
Här är parentesen (x − 2) en gemensam faktor och kan tas utanför en gemensam parentes. |
Lägg märke till att parentesen (x − 2) förekommer två gånger när vi har faktoriserat klart. x = 2 är därför en dubbellösning och vi har bara två olika. De är: x = 2 och x = −2.
Exemplen som vi tittat på hittills är alla ekvationer där termen med den högsta potensen har koefficienten 1.
Hur tar du itu med ekvationer där koefficienten är något annat tal?
Den generella formen är f(x) = ax3 + bx2 + cx + d där a, b, c, och d är heltal.
Vi kan leta efter heltalslösningar på samma sätt som förut genom att testa faktorerna av den konstanta termen d. Om vi hittar en heltalslösning så kan vi dividera och hitta andra lösningar som förut.
Om ingen av faktorerna till d ger oss en lösning då letar vi efter lösningar som är bråk.
Låt oss anta att det finns en lösning som är en fraktion och låt oss kalla denna lösning x = t/n.
Detta betyder att x − t/n är en faktor av f(x), eller, eller om vi multiplicerar med n så är xn − t en faktor.
Låt oss nu anta att vi har dividerat f(x) med xn − t och har hittat andragradsfaktorn, vi kan kalla den
Ax2 + Bx + C.
Nu har vi resultaten som
ax3 + bx2 + cx + d = (xn − t )( Ax2 + Bx + C )
när vi jämför koefficienterna av x3 på båda sidor av ekvationen så ser vi att a = nA och därför måste n vara en
faktor av a.
På samma sätt, när vi jämför de konstanta termerna, ser vi att d = −tC och
därför är t en faktor av d.
Vi bestämmer att ett bråk som är en lösning av tredjegradekvationen ax3 + bx2 + cx + d måste vara av formen t/n där t är en faktor av talet d och n är en faktor av talet a.
Generaliserande för en funktion av graden n:
f(x) = anxn + an−1xn−1+ ∙ ∙ ∙ ∙ + a1x + a0
med koefficienter a0, a1, a2, ∙ ∙ ∙ ∙ ∙ an−2, an−1 och an
Om denna funktion har en rationell lösning, t.ex. t/n, då är t en faktor av a0 och n är en faktor av an .
Exempel 4
Lös ekvationen f(x) = 2x3 − 7x2 + 4x + 3 = 0.
De möjliga heltalsrötterna av f(x) är faktorerna av 3, dessa är ±1 och ±3. Bråken som kan vara rötter av dessa tal är dessa fyra tal dividerat med faktorerna av 2. Så den kompletta listan utav heltal som vi måste överväga är ±½, ±1, ±3/2 and ±3.
Vi kan se på en gång att vi inte behöver överväga några negativa värden eftersom de kommer ge negativa värden för f(x), inte 0.
Låt oss nu prova de andra möjligheterna
f(½) = 2(½)3 − 7(½)2 + 4∙½ + 3 = 3½
f(1) = 2∙13 − 7∙12 + 4∙1 + 3 = 2
f(3/2) = 2(3/2)3 − 7(3/2)2 + 4∙3/2 + 3 = 0 så vi har hittat en lösning.
x = 3/2 är en lösning så (x − 3/2) är en faktor. Att dividera med (x − 3/2) kan vara svårt. Så vi multiplicerar med 2 och dividerar sedan med (2x − 3) istället. Om (x − 3/2) är en faktor så är även (2x − 3) det.
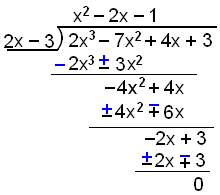
Vi måste nu lösa ekvationen
x2 − 2x − 1 = 0. Vi har redan löst denna ekvation i exempel 2.
Lösningarna var 1 + ![]() 2
og 1 −
2
og 1 − ![]() 2.
2.
Så vi har hittat tre lösningar. De är:
x = 3/2 = 1½
x = 1 + Ö2
x = 1 − ![]() 2
2
Prova test 2 på Ekvationer III.
Kom ihåg att använda checklistan för att hålla ordning på ditt arbete.