© 2008  Rasmus ehf    och
Jóhann Ísak Pétursson

Exponenter och logaritmer.

Lektion 3     Naturliga logaritmer

Då miniräknare och datorer har blivit verktyg för de flesta numeriska operationer, har logaritmer med basen 10 blivit mindre användbara. Fast å andra sidan har en annan logaritm med en annan bas än 10 blivit allt mer användbar i många av vetenskaperna.

Denna funktion kallas den Naturliga Logaritmfunktionen och har symbolen ln.

 f(x)=ln x

Basen för naturliga logaritmer är ett nummer e som du kan se på din räknare.

e är ett irrationellt tal e2.718

Exempel 1

Så här finner du den naturliga logaritmen av 2 på en CASIO-kalkylator:

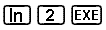
Svaret är ungefär lika med 0.693 vilket är potensen som vi behöver höja e till för att få 2.

   e0.693 2

Kontrollera detta på din kalkylator:

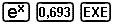
Det givna svaret är 1.9997 2.

Funktionerna f(x) = ln x och g(x) = ex stryker ut varandra när en funktion används på resultatet av den andra. Detta är samma sak som händer med f(x) = log x and g(x) = 10x  eller när man kvadrerar ett tal och sedan tar kvadratroten ur resultatet. Med andra ord så är funktionen f(x) = ln x inversen av funktionen g(x) = ex.

Följande är sant:

    ln ex = x och eln x = x

Talet e är irrationellt och vi kan därför inte finna något exakt värde för det.

Vi kan kalkylera dess värde till vilket antal decimaler som helts genom att välja större och större värden på x för att sedan sätta in dem i följande formel.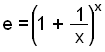

Exempel 2

Räkna ut e genom att sätta in x = 1000 in i formeln och använda en kalkylator.

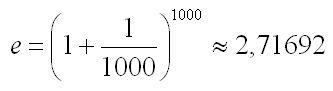
Genom att använda EXCEL får vi värdet 2.7182818284591 för e. Så att välja x = 1000 ger oss endast två korrekta siffror. Prova nu att räkna ut e genom att använda x = 1000000.

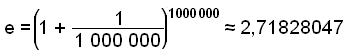
Nu har vi fem korrekta siffror. Ju högre x-värde desto större exakthet i vår beräkning av e.

Exempel 3

Rita graferna till funktionen f(x) = ln x och g(x) = ex.

Gör först en värdetabell:

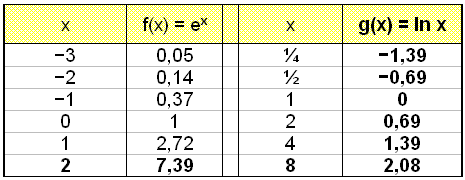
Notera att det inte finns några negativa värden i kolumnen för g(x) = ex och det finns inga negativa värden i x-kolumnen för den inversa funktionen g(x) = ln x.

Definitionsmängden för f(x) = ln x är mängden Ff = { x R | x > 0 }.

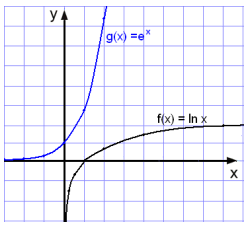
Notera att när vi ritar båda graferna i samma koordinationssystem så är de varandras spegelbild (symmetriska) i en linje dragen genom punkterna där y = x.

Detta är sant för graferna för vilka två funktioner som helst som är varandras inverser.

Samma regel gäller för den naturliga logaritmfunktionen

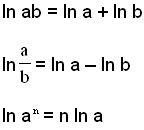
Följande exempel visar hur regeln används.

Exempel 4

Lös följande ekvationer:

a)

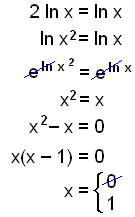Flytta 2 och skriv som en potens. Stoppa in bastalet e på båda sidor av ekvationen.

e och ln stryker ut varandra och lämnar oss med en kvadratekvation.

Flytta x över likhetstecknet. Faktorisera och lös för x

   x = 0 är omöjligt då det inte finns något sätt att skriva 0 som en potens.

b)

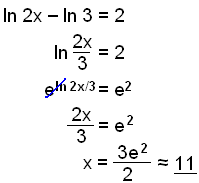Skriv vänstersidan som en logaritm.

Stoppa in bastalet e. ln och e stryker ut varandra.

c)

 

Förenkla den vänstra sidan genom att skriva som en logaritm.

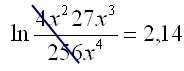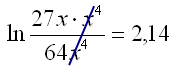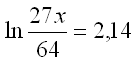Stoppa in basen e på båda sidor.

Exempel 5

Lös följande ekvationer:

a)

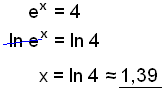Ta logaritmen för båda sidor.

b)

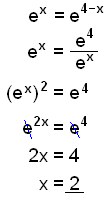Använd reglerna: a x− y = ax/ay.

och  (a n)m = a nm.
För att skriva varje sida som en potens av e.

c)

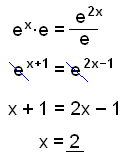Använd reglerna:
a x∙a y = a x+y och a x/a y = a x−y För att skriva varje sida som en potens av e.

Exempel 6

Solve the equations:

a)

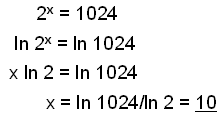Ta log för båda sidorna av ekvationen och använd sedan regeln

a x= x ln a för att flytta det okända värdet ned framför ln.

b)

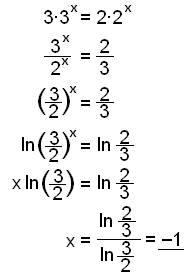Ta termerna med x till ena sidan av ekvationen och de andra termerna till den andra sidan. Förenkla genom att använda reglerna för index.

Ta slutligen log på båda sidor för att flytta ned x och lösa för x. 

c)

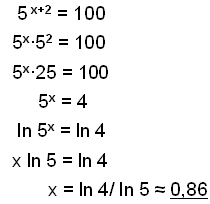Separera potenserna med basen 5. Dividera båda sidor med 25 och lös sedan för x, som förut.

Prova Test 3 på exponenter och logaritmer.

Kom ihåg att använda checklistan för att hålla ordning på ditt arbete.