© 2007  Rasmus ehf    och Jóhann Ísak

Mängder Introduktion 3

Introduktion 3

Reella talen

Vi kan se på tallinjen ( x-axeln) som en kontinuerlig rad med punkter. Varje punkt på linjen utmärker avståndet från den punkten till utgångspunkten (origo). Vi använder ett minustecken (−) om punkten ligger till vänster om origo och ett plustecken (+) om punkten ligger till höger om origo.

Mängderna av tal N och Z är inte de enda talen på linjen. De betecknar endast några tal.

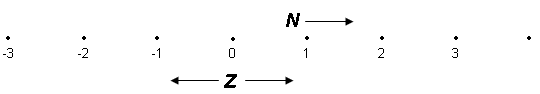
Mängderna av rationella tal Q finns också bland talen på linjen men det finns fortfarande andra tal. Det finns oändligt många tal emellan dem vi redan har behandlat vilka inte kan skrivas som bråk och finns därför inte med i de mängderna vi har haft att göra med.

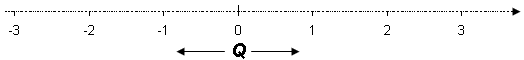
De talen som saknas kallas irrationella tal. De är tal som har ett oändligt antal siffror efter decimaltecknet men där siffrorna inte upprepar sig själva i något mönster och är därför inte periodiska. Här är några exempel.

0,909009000900009
0,123456789101112
	= 1,41421356237
	= 1,73205080756
	= 3,141592653589

  De irrationella talen tillsammans med Q (som innehåller mängderna Z och N) utgör den kontinuerliga linjen utav tal som vi känner till som den reella tallinjen (x-axeln). Tillsammans utgör dessa mängder de Reella talen vilka symboliseras utav bokstaven R.

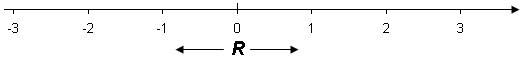
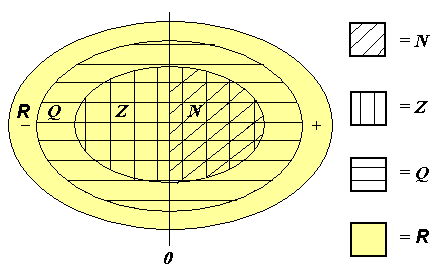
Följande diagram visar förhållandet mellan mängderna R, Q, Z och N. Mängden R innehåller de andra mängderna och kan delas in i rationella tal och irrationella tal. Den delen av diagrammet som inte är markerat med linjer innehåller de irrationella talen. Den delen som är markerad med horisontella linjer visar de rationella talen (mängden Q). Mängden Q delas in i hela tal (mängden Z) och bråk som inte är hela tal. Slutligen delas Z in i hela positiva tal (mängden N) och negativa tal med noll.

Vi kan beskriva intervaller på den reella tallinjen på olika sätt. T.ex. intervallen mellan 1 och 5 inklusive både dessa tal kan skrivas på följande sätt:

Med en olikhet:             1  x 5

Med mängdbeteckningar:     { x R | 1  x  5 }

Med ett diagram:

Ett annat sätt är genom att introducera nya symboler som kallas hakparenteser. Exemplet ovan kan skrivas:

                          [1; 5] eller [1, 5] (det beror på vilken textbok man använder sig av)

Ett intervall såsom [1; 5] där båda ändpunkterna är med kallas för ett slutet intervall.

T.ex. talen som är mindre än 5 men större än 1.

Med en olikhet:                       1 < x < 5

Med mängdbeteckningar:       { x  R | 1 < x < 5 }

Med ett diagram:         

Hakparenteser:

eller [1,5] (beroende på vilken textbok man använder)

Lägg märke till att diagrammet har öppna cirklar eller hål i ändarna för att markera att vi inte inkluderar siffrorna 1 och 5.

Lägg även märke till att vi använder en annan typ av parentes för att visa att ändpunkterna inte är inkluderade.

Intervaller som

där inga av ändpunkterna är inkluderade kallas för öppna intervall.

Slutligen tittar vi på intervaller där endast en ändpunkt behövs.

T.ex. om x är större eller är lika med 1 kan vi skriva:

En olikhet:                       x ≥ 1

Med mängdbeteckningar:       { x R | x ≥ 1}

Diagram:

Intervall beteckningar:

eller [1, ∞[  (återigen så varierar det i textböcker)

Denna typ av intervall kallas för ett halvöppet (eller halvstängt) intervall. Halvöppna intervall fortsätter inte alltid oändligt.

T.ex. intervallet

där 1 inkluderas med 5 inte gör det, är halvöppet. Diagrammet nedan visar detta intervall.

Pröva förhör 3 på ekvations mängder 1.

Kom ihåg att använda checklistan för att hålla ordning på ditt arbete.