© 2007  Rasmus ehf    och Jóhann Ísak Pétursson

Mängder

Introduktion 2 Numeriska mängder

Ett flertal numeriska mängder (dvs. mängder bestående av tal) förekommer ofta i matematik. Detta diagram visar relationen mellan dem.

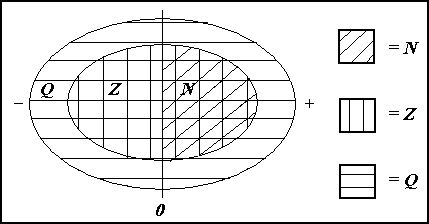
Den enklaste mängden är den med Naturliga tal. Bokstaven N används alltid då man talar om denna mängd. N = { 1,2,3,∙∙∙ }. Detta är talen vi använder för att räkna och de fortsätter i oändlighet. Noll är ofta inkluderat i denna mängd.  Detta visas genom att sätta 0 som ett index till N.

N₀ = { 0,1,2,3,∙∙∙ }.

Bokstaven Z används för att symbolisera mängden av alla hela tal, positiva och negativa.

Z = {∙∙−2,−1,0,1,2,∙∙}.

Mängden N är en äkta delmängd till Z.

N Z

Den tredje mängden vi talar om symboliseras av bokstaven Q från ordet Quotient. Detta är mängden av alla rationella tal, eller, med andra ord: mängden av alla bråk som kan skrivas med hela tal i nämnaren och täljaren. Lägg märke till att alla hela tal även kan skrivas som bråk, så både Z och N är äkta delmängder till Q.

Z    Q och N   Q

Lägg märke till att alla elementen i dessa tre mängder kan skrivas genom att använda hela tal.

Nu ska vi behandla decimaler.

Exempel 1

Skriv

och

som decimaler

Genom att använda en kalkylator och dividera 1 med 3 får vi

 0,333∙∙∙∙

 0,1212∙∙∙∙

Decimalerna i dessa exempel har en oändlig mängd siffror efter decimaltecknet. Samma ordningsföljd av siffror upprepar sig självt om och om igen. Detta kallas periodisk decimalutveckling.

I det första exemplet består perioden utav en siffra, talet 3. I det andra exemplet består perioden utav 2 siffror (1 och 2 som upprepas). Alla rationella tal kan skrivas som periodiska decimalutvecklingar.

Dessa exempel visar hur ett bråk kan ändras om till decimalform genom division. Nu ska vi se hur en decimalform ändras till ett bråk.

Om decimalformen har en fast andel tal så kan vi ändra den till ett bråk genom att flytta decimaltecknet tills vi har ett helt tal och sedan dividera med 10, 100, 1000…beroende på hur många placeringar vi flyttat decimaltecknet.

Exempel 2

Skriv 0,3, 0,12 och 0,1212 som bråk.

0,3

=

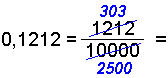Denna metod fungerar inte med periodiska decimalutvecklingar som har ett oändligt antal siffror efter decimaltecknet. I dessa fall måste vi använda en annan metod.

Exempel 3

Ändra 0,333∙∙∙∙∙, 0,1212∙∙∙∙∙ och 1,14333∙∙∙∙ till bråk.

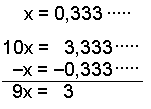		Kalla talet X. När perioden består utav en siffra multiplicerar vi talet med 10 vilket ger oss 10x. Subtrahera nu det originella talet från 10x. På detta sätt elimineras alla siffrorna efter decimaltecknet.
		Slutligen divideras svaret med 9 för att finna x. Eliminera om möjligt.

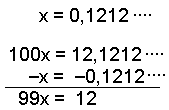		Kalla talet x. Denna gång har perioden två siffror så vi multiplicerar talet med 100 och får 100x.  Subtrahera nu det originella talet från 100x.
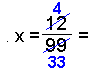
		Återigen elimineras samtliga siffror efter decimaltecknet. Slutligen divideras svaret med 99 för att finna x. Eliminera om möjligt.

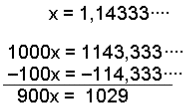		I detta exempel måste vi börja med att multiplicera med 100 så att perioden börjar direkt efter decimaltecknet. Denna gång är perioden endast en siffra så vi multiplicerar igen med 10. Nu subtraherar vi 100x från 1000x så att siffrorna efter decimaltecknet elimineras.
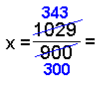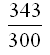		Slutligen dividerar och eliminerar vi för att hitta originella x.

Pröva förhör 2 på Mängder (Sets)   I.  
Kom ihåg att använda checklistan för att hålla ordning på ditt arbete.