© 2009  Rasmus ehf    och Jóhann Ísak

Funktioner 2

Introduktion 1

Sammansatta funktioner

Det finns många kombinationer av funktioner. Vi kommer att titta lite närmare på några av dem här nedan. 

Exempel 1

De angivna funktionerna är f(x) = x2 + x och g(x) = x + 1.

a)   Hitta summan av f och g.

          f(x) + g(x) = (x2 + x) + (x + 1) = x2 + 2x + 1

b)   Hitta differensen av f och g.

          f(x) - g(x) = (x2 + x) – (x + 1) = x2 + x –x – 1 = x2 – 1

c)   Hitta 2f(x) – 3g(x).

          2f(x) – 3g(x) = 2(x2 + x) – 3(x + 1) = 2x2 + 2x – 3x – 3

                               = 2x2 – x – 3

d)   Multiplicera f och g.

          f(x)·g(x) = (x2 + x)·(x + 1) = x3 + x2 + x2 + x = x3 + 2x2 + x

e)   Dividera f och g.

Resultatet av divisionen är linjen y = x, men observera att definitionsmängden för funktionen f(x)/g(x) = x är begränsad då du inte kan använda x = –1 eftersom nämnaren blir då lika med 0. Om definitionsmängden för både f och g är alla reella tal, även skrivet som R, då blir f(x)/g(x) = Df/g = R\{–1}. Grafen för f(x)/g(x) blir en rät linje y = x med ett hål där x = –1.

Nu ska vi se vad som händer ifall vi använder en funktion, exempelvis g istället för variabeln x och en annan funktion, exempelvis f, på resultatet. Att sätta ihop funktionerna f och g på det här sättet kallas för sammansatta funktioner och skrivs f(g(x)) (läses som f utav g utav x) eller f o g. Nu ska vi titta lite närmare på några sammansatta funktioner där funktionen för g används först istället för x och funktionen f använder sedan resultatet utav det.

Exempel 2

De angivna funktionerna är f(x) = x2 + x och g(x) = x + 1.

a)  Hitta f(g(x)).

        f(g(x)) = (x + 1)2 + (x + 1) = x2 + 2x + 1 + x + 1 = x2 + 3x + 2

b)  Hitta g(f(x)).

        g(f(x)) = x2 + x + 1

c)   Hitta f(f(x)).

        f(f(x)) = (x2 + x)2 + (x2 + x) = x4 + 2x3 + 2x2 + x

d)   Hitta g(g(x)).

        g(g(x)) = (x + 1) + 1 = x + 2 

I sammansatta funktioner som exempelvis f(g(x)), kallas g(x) inre funktion och f(x) yttre funktion. När vi sätter ihop funktioner används den inre funktionen istället för variabeln i den yttre funktionen.

Exempel 3

De angivna funktionerna är  f(x) = och  g(x) = x2 + 1.

a)  Hitta f(g(x)).

        f(g(x)) =

b)  Hitta g(f(x)).

        g(f(x)) = = x + 1

Vi har tidigare tittat lite på förflyttningar av funktioner. Vi kan även se att förflyttning är en variant av sammansatt funktion. Vi tittar lite närmare på detta i nästa exempel.

Exempel 4

Vi önskar förflytta grafen av funktionen f(x) = x3 – x med vektorn .

I följande värdetabell antar x värdena mellan -2 och 2. Först räknar vi f(x). Sedan förflyttar vi alla resultat ner med 1 (det vill säga att värdet för x = -2 blir x = -1). Detta blir likvärdigt med att räkna ut värdena för f(x–1). Slutligen adderar vi alla resultat med 3 (vilket är likvärdigt att funktionen förflyttas med 3).

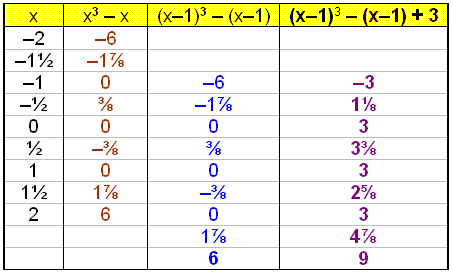
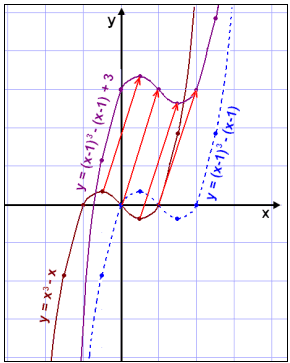
Vi kan se på diagrammet att förflyttningen af grafen f(x) är en enhet till höger vilket ger oss grafen f(x-1)(se den blåa grafen). När vi adderar den funktionen för den blåa grafen med 3 förflyttas den 3 enheter uppåt. Då har varje punkt i orginalgrafen f(x) förflyttats med vektorn ..

Följande regler gäller:

Förflyttning av grafen f(x) med vektorn

ger oss grafen f(x–a) + b.

Exempel 5

Vi tittar nu på  funktionerna  f(x) = och g(x) = 4 – x2 och hittar definitionsmängden samt värdemängden för de sammansatta funktiorna.

Vi måste uppenbarligen begränsa värdet inom kvadratroten till enbart poritiva tal. Därför kan sen sammansatta funktionen f(g(x)) = enbart anta positiva värden av den inre funktionen g(x) = 4 – x2. Detta innebär att vi måste begränsa definitionsmängden av den inre funktionen g(x) så att värdemängden (resultatet) av funktionen enbart blir positiva tal. Titta på grafen g(x) = 4 – x2 med detta i åtanke. Värdetabellen blir följande:

x g(x) = 4 - x2
-3 -5
-2 0
-1 3
0 4
1 3
2 0
3 -5

Grafen ser då ut så.

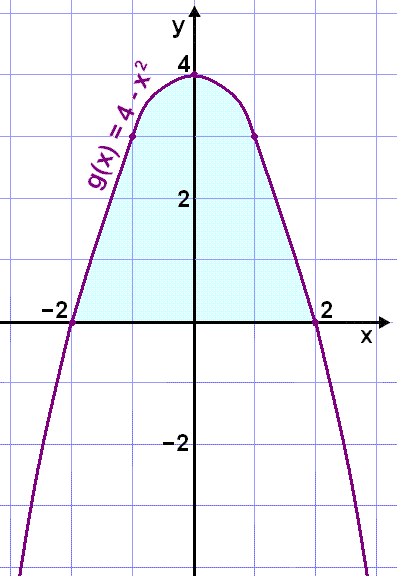
Det färgade området av grafen visar var g(x) ligger ovanför x-axeln. Med intervallet -2 och 2 har den inre funktionen g(x) de positiva talen 0 till 4. Om vi väljer definitionsmängden av g(x) eller D g(x) = {x R | –2 ≤ x ≤ 2} då får vi värdemängden Vg(x) = {y R | 0 ≤ y ≤ 4}. Denna mängd blir sen definitionsmängden för f(x) i den sammansatta funktionen.  Om vi väljer värden för x med intervallet 0 ≤ x ≤ 4, då tar f(x) värdena mellan 0 ≤ x ≤ 2.

Vi har nu visat att definitionsmängden av f(g(x)) blir Df(g(x)) = {x R | –2 ≤ x ≤ 2} och värdemängden f(g(x)) blir Vf(g(x)) = {y R | 0 ≤ x ≤ 2}. Slutligen låt oss titta på grafen.

Först värdetabellen.

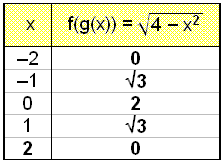
Grafen blir en halv cirkel med mitten i (0, 0) och radien 2.

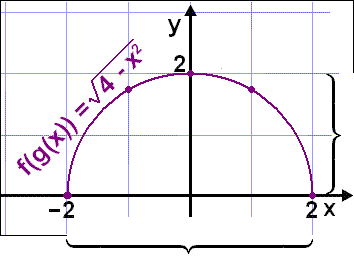Vf(g(x)) = {y R | 0 ≤ x ≤ 2},

         Df(g(x)) = {x R | –2 ≤ x ≤ 2 }

Här är några punkter för att hitta definitionsmängden och värdemängden av sammansatta funktioner.

1)   Välj definitionsmänden av den inre funktionen så attvärdemängden kan användas som definitionsmängd av den yttre funktionen. 
     

2)   Använd denna definitionsmängd för att hitta värdemängden för den yttre funktionen.
     

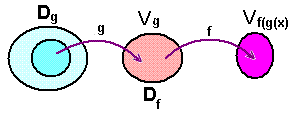
Ibland kan, som exemplet ovan visar, enbart delar av definitionsmängden för g användas. De värden som värdemängden fær g antar utifrån denna definitionsmängd blir definitionsmängd för den yttre funktionen f. Värdena som f antar utifrån definitionsmängden blir värdemängden för den sammansatta funktionen f(g(x)).

Öva på detta och ta sen test 1 i funktioner 2.

ps. Kom ihåg att använda checklistan för att hålla ordning på ditt arbete.