Funktioner I
| © 2007 Rasmus ehf och Jóhann Ísak Pétursson |
Funktioner I |
Rationella funktioner
Rationella funktioner har följande
form:
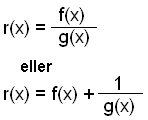
Där f(x) och g(x) båda är polynom och nämnaren,
g(x) har en gradbeteckning på minst ett (innehåller ett x).
Vi ska nu titta på några exempel på rationella
funktioner och deras grafer.
Exempel 1
Titta först på
![]()
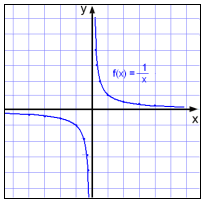
Om vi börjar med att göra en
värdetabell så ser vi på en gång att x inte kan vara värdet 0 eftersom det
innebär att dividera med 0.
Allt eftersom x kommer närmare
och närmare värdet 0 men är fortsatt positivt (
x= 0.1 , x = 0.01 osv...)så ser vi att funktionsvärdet (y-värdet) blir större
och större ( x = 0.01 ger oss
y= 100).
Allt eftersom x kommer närmare
och närmare 0 men är fortsatt negativt ( x = −0.1, x =− 0.01
osv..)
får funktionsvärdet ett större
och större negativt värde ( x = −0.01 ger oss y= −100).
När detta händer så säger
man att funktionen har en vertikal asymptot
Ekvationen till asymptoten är
x = 0.
Exempel 2
Sedan ska vi undersöka
funktionen
![]()
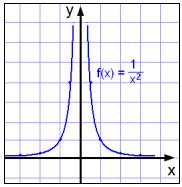
Vi ser att värdet på
funktionen blir större och större allt eftersom x närmar sig 0 från höger (
x > 0 ) och från vänster ( x < 0 )
Återigen är y-axeln en
vertikal asymptot.
Vi kan försöka att beräkna
dessa skärningspunkter och se vad som händer.
Vi finner vart grafen skär
y-axeln genom att räkna ut f(0), där x-koordinaten för alla punkter på
y-axeln är 0.
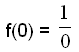
För att räkna ut detta måste
vi dividera med 0, vilket är omöjligt.
För att finna vart grafen skär
x-axeln måste vi lösa ekvationen f(x) = 0 eller y = 0 därför att alla
punkter på x-axeln har y-koordinaten 0.
| = 0 | |
|
1 = 0∙x2 |
|
Återigen får vi en ekvation
som inte kan lösas. Vi kan därför dra slutsatsen att grafen inte skär
koordinataxlarna.
Exempel 3
Titta på funktionen
![]()
och kalkylera vart grafen skär
axlarna.
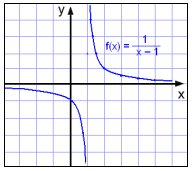
Om x = 1 kommer vi dividera med
0 och därför är x ≠ 1. Då x kommer närmare och närmare 1 blir y-värdet
större och större, positivt om x>1 och negativt om x<1.
Denna gång verkar grafen ligga
nära linjen genom x = 1 och gå uppåt när x > 1 och nedåt när
x < 1.
För att finna vart grafen skär y-axeln räknar vi ut
f(0), då x = 0 på y-axeln.
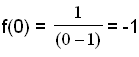
För att finna vart grafen skär
x-axeln löser vi ekvationen f(x) = 0 eller y = 0 då alla punkter på x-axeln
är y = 0.
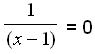
1 = 0∙(x − 1) = 0
Återigen får vi en ekvation
som inta har ngn lösning så vi kan dra slutsatsen att grafen inte skär
x-axeln.
Exempel 4
Titta på funktionen
![]()
och hitta några skärningspunkter
med koordinataxlarna.
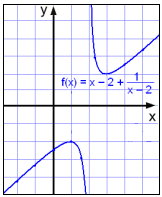
Vi ser att x ≠ 2 då vi i
så fall skulle ha 0 i nämnaren. Då x närmar sig 2 från höger i så blir
funktionsvärdet större och större och grafen går uppåt. Då x närmar sig 2
från vänster får funktionen ett större och större negativt värde och
grafen går nedåt.
Så grafen har en vertikal asymptot x = 2.
Grafen skär y-axeln när x = 0
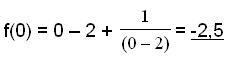
Grafen skär y-axeln när f(x)
= 0. Vi måste lösa ekvationen:
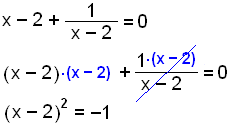 |
När vi multiplicerar genom med (x - 2) så får vi en ekvation som inte har någon lösning. |
Eftersom ekvationen f(x) inte
har någon lösning skär inte grafen x-axeln.
Exemplen ovan visar att en
rationell funktion nästan alltid har en vertikal asymptot vid punkten där nämnaren
är noll. (De enda undantagen är när vi kan faktorisera bråket och stryka ut
nämnaren). Funktionen kan beräknas för alla andra värden på x.
Exempel 5
Slutligen ska vi utreda
funktionen
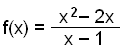
och finna den vertikala asymptoten och punkterna där
grafen skär x- och y-axlarna.
Börja med att överväga för
vilka x-värden vi inte kan räkna ut f(x). Nämnaren är noll när x − 1
= 0, med andra ord när x = 1.
Den vertikala asymptoten är där
x = 1 och funktionen gäller för alla värden på x förutom x = 1. Genom att
använda mängdbeteckningar kan vi skriva.
{xÎR| x ¹ 1} eða R \ {1}
Finn sedan y-interceptet genom
att räkna ut f(0).
f(0) = (0 − 0)/(0 − 1) = 0
Grafen skär y-axeln i (0,0).
För att finna vart grafen skär
x-axeln måste vi lösa ekvationen f(x) = 0.
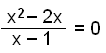 |
|
x2 − 2x = 0∙(x − 1) = 0
x(x − 2) = 0
x = 0 eller 2
Grafen skär x-axeln där x = 0
och x = 2.
Pröva förhör 4 på Funktioner I.
Kom ihåg att använda checklistan för att hålla
ordning på ditt arbete.