Funktioner I
| © 2007 Rasmus ehf och Jóhann Ísak |
Funktioner I |
Lektion 3
Andragrads funktioner
Låt oss titta på andra gradens polynomer. Den
enklaste formen utav funktionen är f(x) = x2. Grafen är en parabel
ofta kallad basparabeln.
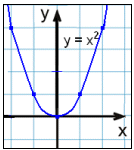
Lägg märke till att grafen är symmetrisk i förhållande
till y-axeln. Y-axeln kallas för symmetriaxel i denna funktion.
Nu ska vi se hur koefficienterna påverkar
utseendet på grafen.
Koefficienten i x2 kallas vanligtvis för a. Om vi tittar på parablerna med
olika värden på a så ser vi att vissa är bredare och andra smalare än
basparabeln där a = 1.
Här är grafer med parabler där a = 4, 2, ½
och ¼.
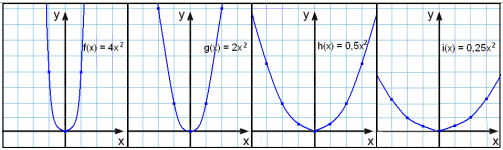
a = 4 a = 2 a = ½ a = ¼
Här är parabler med negativa
värden på a
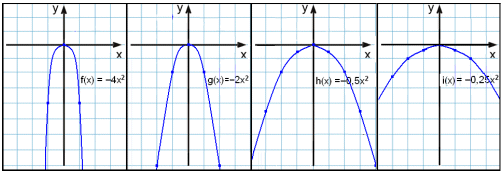
a = −4 a = −2 a = −½ a = −¼
Om värdet på a är positivt så
böjer sig grafen uppåt (som ett leende). Ju större värdet på a är ju
smalare blir grafen.
Allt eftersom a blir mindre blir grafen flatare och
flatare till den blir negativ och böjer sig nedåt (som en sur min).
Exempel 1
Nu ska vi rita grafen för f(x) = x2 + 1 och jämföra den med g(x) = x2.
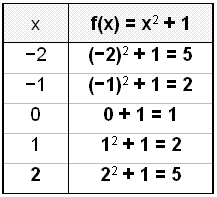 |
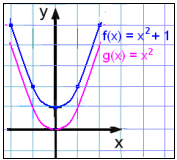 |
Värdena på funktionen (y-värdena)
i värdetabellen för f(x) = x2 +1 är alla ett högre än motsvarande värden i värdetabellen för
g(x) = x2 och grafen har förflyttats
vertikalt med 1 enhet.
Lägg märke till att grafen för
f(x) = x2 + 1 inte skär x-axeln. Detta talar om för oss att
ekvationen x2 + 1 = 0 inte någon lösning. Detta vet vi eftersom ett
tal i kvadrat aldrig är negativt, så x2 kan aldrig bli lika med -1.
Exempel 2
Rita grafen för f(x) = x2
− 1 och jämför den med g(x) = x2.
 |
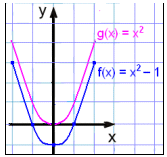 |
Nu är alla funktionsvärden i
f(x)-tabellen ett lägre än motsvarande värden i tabellen för g(x) = x2
och grafen har förflyttats ned med en enhet.
Lägg märke till att i detta
exempel skär grafen till f(x) = x2 − 1 x-axeln på två ställen.
Detta betyder att ekvationen x2
− 1 = 0 har två lösningar,
x2 − 1 = 0
x2 = 1
x = ±1
vilka är x = −1 og x = 1.
Exempel 3
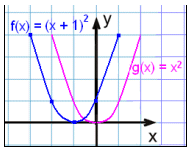
Rita grafen till f(x) = (x + 1)2
( eller f(x) = x2 +
2x + 1) och jämför den med grundparabeln g(x) = x2.
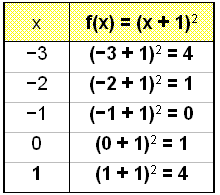 |
 |
Här har vi lagt till 1 till x
och vi kan se att alla funktionsvärdena i tabellen med värden har flyttat upp
en rad i jämförelse med basfunktionen.
Grafen till f(x) är densamma
som grafen till g(x) = x2 om
vi flyttar den en enhet till vänster.
Vi säger att basgrafen har
blivit förskjuten med -1 enheter horisontellt. Symmetriaxeln är nu x = -1.
Exempel 4
Rita grafen till f(x) = (x − 2)2
− 1 (eller f(x) = x2 − 4x + 3) och jämför den med
basgrafen g(x) = x2.
Om vi använder samma metod som i föregående
exempel kan vi anta att grafen har förflyttats två enheter till höger och en
enhet nedåt. Nu ska vi kolla upp detta genom att göra en värdetabell och börja
med x = 0 och rita grafen.
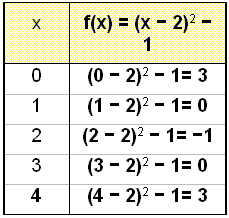 |
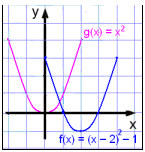 |
Lägg märke till att symmetriaxeln nu är x = 2.
Vi kan finna vart grafen går över y-axeln utan
att rita grafen. Vi gör detta genom att beräkna f(0)
= 3 eller genom att multiplicera bort
parenteserna och se att den konstanta termen (termen utan x) är 3.
f(x) = (x − 2)2 − 1 = x2 − 4x + 4 − 1 = x2 − 4x + 3
eller f(0) = (x − 2)2 − 1 = 4 − 1 = 3
Exempel 5
Hitta vart grafen för f(x) = (x − 2)2
− 1 skär x-axeln. Vi sätter y = f(x) = 0 och löser ekvationen för x.
| (x − 2)2 − 1 = 0 | Flytta först -1 till andra sida med likhetstecknet. |
| (x − 2)2 = 1 | Sedan tar du ut kvadratroten ur båda sidorna av ekvationen. Kom ihåg + och -. |
| x − 2 = ±Ö1 = ±1 | Flytta slutligen 2 över till andra sidan och förenkla resultatet. |
| x = 2 ± 1 |
Skärningspunkterna är x = 2 −1 = 1 och x = 2 + 1 = 3.
Det är lätt att se att när man skriver
funktionen som f(x) = (x − 2)2 − 1 så får man en massa
information.
Det talar om för oss hur basgrafen förflyttas
vertikalt och horisontellt.
Det talar också om för oss vart symmetriaxeln
finns.
Slutligen så kan vi enkelt finna skärningspunkterna
på x- och y-axlarna.
Den generella formen för ekvationen skriven i
denna form är:
f(x) = a(x + r)2 + s
a är koefficienten av x2 som vi redan
sett.
Symmetriaxeln har ekvationen x
= −r (eller så kan man säga att den har samma värden som r men med
motsatta tecken).
På grund utav detta är det viktigt att veta hur
man skriver om funktionen
f(x) = ax2 + bx + c till formen f(x) = a(x + r)2 + s
Exempel 6
Låt oss nu titta hur vi kan ändra en andragrads
funktion från en form till en annan. Skriv om f(x) = x2 − 4x +
3 till formen f(x) = (x − 2)2 − 1.
f(x) = ax2 + bx + c
f(x) = x2 − 4x + 3
Här är a = 1
och b = −4
och c = 3 (så grafen skär y-axeln vid 3).
Titta på regeln för att kvadrera en parentes:
Vi
ser att koefficienten för x är 2q.
I
vårt exempel är koefficienten av x -4 vilket betyder 2q = − 4 och därför
är q = −2.
Om vi räknar ut (x − 2)2
får vi x2 − 4x + 4
(x − 2)2 = x2 − 4x + 4.
Om
vi subtraherar 1 från båda sidorna får vi:
(x − 2)2
−1 = x2 − 4x + 4−1 = x2 − 4x + 3
Summerande av metoden:
| f(x) = x2 − 4x + 3 | Halva koefficienten utav x är −4/2 = −2 som vi kvadrerar (4 ) och lägger till ekvationen. |
| = (x2 − 4x + 22) − 22 + 3 | |
| = (x − 2)2 − 4 + 3 | Om vi lägger
till 4 till ekvationen måste vi även dra bort 4 så att ekvationen förblir
oförändrad. Nu förenklar vi −4+3 = −1 |
| = (x − 2)2 − 1 |
Från exemplet ovan kan vi dra slutsatsen att
grafen till ett andra gradens polynom där a = 1 (f(x) = x2 + bx + c)
har sin symmetriaxel i:
x = −b/2 och skär y-axeln där y = c.
Exempel 7
Hitta symmetriaxeln till grafen för f(x) = 2x2
− 12x + 10.
I detta fall är a = 2 så regeln från det föregående
exemplet gäller inte. Det är inte heller lika lätt att skriva om funktionen
som förut.
Istället flyttar vi ned funktionen med 10
enheter genom att subtrahera 10 från ekvationen. Att flytta grafen vertikalt ändrar
inte positionen på symmetriaxeln.
Vi kan kalla denna nya funktion för g(x) och
finna vart g(x) skär x-axeln.
2x2 − 12x = 0
2x(x − 6) = 0
Denna ekvation har lösningen x = 0 och 6 så
grafen till g(x) skär a-axeln i 0 och 6. Symmetriaxeln måste vara i mitten
utav dessa två punkter, dvs. i x = 3.
Exempel 8
Skriv om funktionen f(x) = 2x2 −
12x + 10 i formen
f(x) = a(x + r)2 + s .
| f(x) = 2x2 − 12x + 10 | Ta ut två ur en parentes. Halva koefficienten utav x är −6/2 = −3 så lägg till 32 inuti parentesen. Vi har redan lagt till 18 så nu måste vi subtrahera 2×32 = 18 utanför parentesen. |
| = 2(x2 − 6x + 32) − 2∙32+ 10 | |
| = 2(x2 − 6x + 9) − 18 + 10 | |
| = 2(x − 3)2 − 8 |
Nu ser vi, precis som förut, att symmetriaxeln
är i x = 3.
Koefficienten utav x i exemplet ovan (f(x) = 2x2
− 12x + 10) är a = 2, b = −12 och c = 10. För att finna
symmetriaxeln tog vi faktorn 2 utanför en parentes. Detta motsvarar till att
dividera med 2. Sen fullbordade vi kvadraten genom att dela koefficienten utav x
(−6) med 2
Den generella formeln för symmetriaxeln till
funktionen
f(x) = ax2 + bx + c är därför:
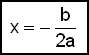
Exempel 9
Finn vertex till parabeln f(x) = 2x2
− 12x + 10.
Vertex ligger (där parabeln kröker sig) på
symmetriaxeln och därför vet vi x-värdet utav vertex (3).
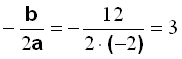
Vi finner y-värdet genom att räkna ut f(3).
Vertex till parabeln är (3, −8).
Notera: Om a>0 så är vertex en minimipunkt.
Om a<0 så är vertex maximipunkt.
Pröva förhör 3 på Funktioner I.
Kom ihåg att använda checklistan för att hålla
ordning på ditt arbete.