© 2000 - 2009 Rasmus ehf & Jóhann Ísak Pétursson

Równania II

 

Prezentacja nr 3 

 Równania kwadratowe


Przykład nr 1

5X2 = 45

      

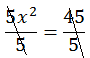
Otrzymujemy wynik X2 = 9

Jeśli równanie zawiera niewiadomą do potęgi drugiej, np. tak  X2 albo tak y2   to po uproszczeniu nazywamy  to równanie „równaniem kwadratowym”.

Wiemy już, że pierwiastek to odwrotność drugiej potęgi.

Otrzymujemy:

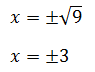
Ponieważ i (-3)2 i 32 = 9


Przykład nr 2

x2 - 5x = 0   Najlepiej rozpocząć rozwiązywanie równania od wyciągnięcia czynnika przed nawias.

x(x - 5) = 0      Jeśli jeden z czynników równy jest zero to równanie jest spełnione.

0(x - 5) = 0    lub  x(0) = 0

x(x - 5) = 0

Jeśli ten czynnik = 0 to znamy pierwsze rozwiązanie.

Zatem x = 0.

Lub x1 = 0

x(x - 5) = 0

Jeśli ten czynnik = 0 to znamy drugie rozwiązanie.

Zatem x – 5 = 0 lub x = +5.

Lub x2 = +5

 

Takie równania mają zawsze dwa rozwiązania, które zazwyczaj nazywamy

x1  i x2 dla rozróżnienia.


Teraz zrób test nr 3.
PS. Pamiętaj, żeby regularnie wypełniać Twoją tabelkę wyników.