|
© 2000 - 2009 Rasmus ehf |
Mnożenie i dzielenie ułamków |
|
Prezentacja nr 1
Skracanie i upraszczanie ułamków
Przypomnijmy sobie
rozkładanie na czynniki.
Przykład: Liczba 6 = 2 · 3. Mówimy, że liczba 6 ma dzielniki 2 i 3. Wszystkie liczby całkowite mają dwa lub więcej dzielników, oprócz liczb, które nazywamy pierwszymi, np. (2,3,5,7,11,13,17,19,23.......itd.)
Liczba 1 nie ma wpływu na mnożenie i dlatego nigdy nie jest używana jako dzielnik.
Pamiętaj, że pozioma kreska zawsze oznacza dzielenie.
Kilka przykładów, jak można korzystać ze wspólnych dzielników przy skracaniu ułamków.
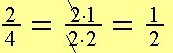Widzimy, że
2 = 2·1
oraz
4 = 2·2
Liczba 2 jest wspólnym dzielnikiem ( 2:2 = 1). Skracamy ułamek przez wspólny dzielnik.
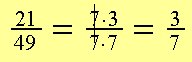Widzimy, że
21 = 7·3
oraz
49 = 7·7
Liczba 7 jest wspólnym dzielnikiem. Skracamy ułamek przez wspólny dzielnik.
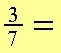Liczby pierwsze nie mają
dzielników oprócz samych siebie i 1.
Nie ma więc wspólnego dzielnika, ułamek jest niemożliwy do skrócenia.
Mnożenie ułamków
Czasami posługujemy się całościami i ułamkami.
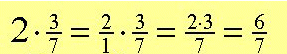
Zamieniamy całość w ułamek a później mnożymy.
Całość jest mnożona tylko przez licznik.
Mnożenie ułamka przez ułamek (nie szukamy wspólnego mianownika).
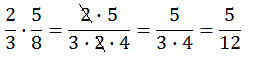
Mnożenie ułamków: licznik · licznik oraz mianownik · mianownik. (Uwaga: 2:2 równa się 1 oraz 1 · 5 = 5)
Liczby mieszane w mnożeniu:
Przykład: Mnożymy całość przez mianownik i dodajemy licznik. 1 · 3 + 1 = 4 i umieszczamy wynik w miejscu licznika. Mianownik się nie zmienia.
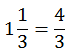
Musimy umieć zamienić liczbę mieszaną w ułamek.
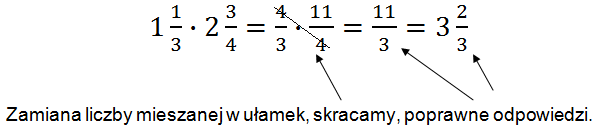
Najpierw zamieniamy w ułamek, skracamy i upraszczamy.
Uwaga: Odpowiedź można zapisać na różne sposoby.
Dzielenie ułamków
Kiedy mnożymy ułamki to obracamy drugi ułamek i obliczamy zadanie jak mnożenie.
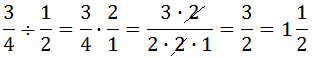
Zaczynamy od obrócenia drugiego ułamka, a potem skracamy wspólne części.
Całości muszą być zmienione w ułamki.
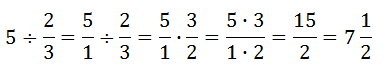
Zamieniamy całość w ułamek.
Umieszczamy na kresce jak przy mnożeniu, lecz najpierw obracamy drugi ułamek.
Liczby mieszane muszą być zmienione w ułamek niewłaściwy.
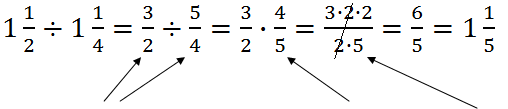
Zamieniamy liczbę mieszaną w ułamek, obracamy drugi ułamek, skracamy.
Teraz zrób test nr 1.