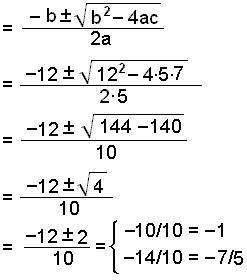© 2009  Rasmus ehf    og Jóhann Ísak

Trygonometria


Drukuj

Prezentacja nr 2  

Funkcje sumy i różnicy kątów oraz wzory na funkcje podwójnego kąta

Wzory na sinus, cosinus i tangens sumy lub różnicy dwóch kątów mogą być bardzo przydatne. Dowody kilku z nich znajdują się poniżej.

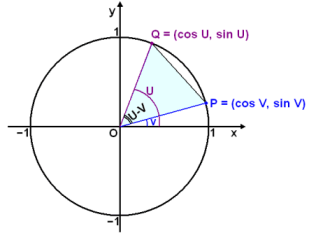
Trójkąt OPQ na obrazku powyżej ma wierzchołki P, Q oraz O, który znajduje się w początku układu współrzędnych. Kąt znajdujący się między osią x oraz OQ nazwiemy u, a kąt między osią x i OP - v. Kąt POQ to zatem u - v. Punkt Q ma współrzędne (cos u, sin u), a punkt P (cos v, sin v). Odległość między P i Q można zapisać jako |PQ|. Aby ją poznać użyjemy wzoru na odległość między dwoma punktami. 

   |PQ|2 = (cos u − cos v)2 + (sin u − sin v)2  

            = cos2u − 2 cos u cos v + cos2v

               + sin2u − 2 sin u sin v + sin2v  

            = 1 − 2 cos u cos v− 2 sin u sin v + 1

            = 2 − 2 cos u cos v − 2 sin u sin v

 

 Przemnażamy
(odległość)2 =
(x2−x1)2 + (y2−y1)2

 

 

Teraz obliczamy |PQ| wykorzystując twierdzenie cosinusów.

   |PQ|2 = 12 + 12 − 2∙1∙1∙cos (u − v)

             = 2 − 2∙cos (u − v)

Przyrównując te dwa wyrażenia do siebie otrzymujemy:

   2 − 2∙cos (u − v) = 2 − 2 cos u cos v − 2 sin u sin v

      − 2∙cos (u − v) = − 2 cos u cos v − 2 sin u sin v

Jeśli podzielimy wszystko przez -2 to otrzymamy następujący wzór:

cos (u − v) = cos u cos v + sin u sin v

Otrzymamy kolejny wzór, jeśli w powyższym równaniu wstawimy -v zamiast v:

   cos (u − (−v)) = cos u cos (−v) + sin u sin (−v)

Wykorzystując zależności dla okręgu jednostkowego cos (−v) = cos v i sin (−v) = − sin v możemy zapisać wyrażenie jako:

cos (u + v) = cos u cos v − sin u sin v

Wymnażamy nawiasy i upraszczamy.

Na rysunku poniżej narysowaliśmy dwa trójkąty. Jeden z nich ma kąt v między przeciwprostokątną a osią x, drugi ma taki sam kąt między przeciwprostokątną a osią y. To oznacza, że te dwa trójkąty są przystające.

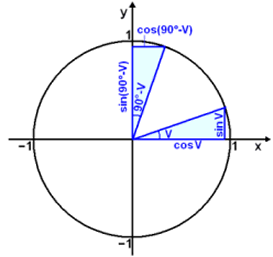
Te dwa przystające trójkąty prowadzą do poniższych zależności:

   cos v  = sin (90° − v)    og   sin v = cos (90° − v)

   cos v  = sin (90° − v)    i   sin v = cos (90° − v)

Teraz w powyższych zależnościach podstawiamy 90°  zamiast u  i (u + v) zamiast v.

    sin (u + v) = cos (90° − (u + v))

                     = cos ((90° − u) − v)

                     = cos (90° − u) cos v + sin (90° − u) sin v

                     = sin u cos v + cos u sin v

W ten sposób znaleźliśmy wzór na sin (u + v):

sin (u+v) = sin u cos v + cos u sin v

Jeśli teraz w tym równaniu podstawimy (−v) zamiast v to otrzymamy:

sin (u − v) = sin (u + (−v))

                    = sin u cos (−v) + cos u sin (−v)

                    = sin u cos v − cos u sin v

Teraz użyjmy wzoru

cos(u−v) = cos u cos v−sin u sin v 
a potem sin v = cos (90° − v)

i cos v  = sin (90° − v).

W ten sposób otrzymaliśmy wzór na sin (u - v):

sin (u-v) = sin u cos v - cos u sin v

 

Przez zamianę v na u we wzorach na sin (u + v) i cos (u + v) otrzymujemy wzory na sin (u + u) i cos (u + u), nazywane wzorami na dwukrotność kąta:
 

sin 2u = 2 sin u cos u

cos 2u = cos2 u − sin2

Wzór na cos 2u może być zapisany na jeszcze dwa sposoby wykorzystując zależność   cos2 u + sin2 u = 1. 

Zastępujemy sin2 u i cos2 przez cos2 u = 1 − sin2 u i sin2 u = 1 − cos2 . Otrzymujemy następujące wzory:

cos 2u = 2 cos2 u − 1

cos 2u = 1 − 2 sin2 u

Przykład nr 1

Użyj powyższych tożsamości, aby znaleźć dokładne wartości sin 15° i cos 15°.

Wiemy już, że cos 45° = Ö2/2, sin 45° = Ö2/2, cos 60° = ˝ i sin 60° = Ö3/2. Wykorzystując tożsamość na cos różnicy kątów otrzymujemy:

   cos 15° = cos (60° − 45°)

                 = cos 60° cos 45° + sin 60° sin 45°

                 = ˝∙Ö2/2 + Ö3/2∙Ö2/2

                 = Ö2/4 + Ö3∙Ö2/4

                 = Ö2∙(1 + Ö3)/4

Wykorzystując tożsamości na sin różnicy kątów otrzymujemy:

     sin 15° = sin (60° − 45°)

                 = sin 60° cos 45° − cos 60° sin 45°

                 = Ö3/2∙Ö2/2 − ˝∙Ö2/2

                 = Ö3∙Ö2/4 − Ö2/4

                 = Ö2∙(Ö3 − 1)/4

Przykład nr 2

Uprość wyrażenie sin (270° − v).

Wykorzystujemy tożsamość sin (u − v) = sin u cos v − cos u sin v.

sin (270° − v) = sin 270° cos v − cos 270° sin v

                       = −1∙ cos v − 0∙ sin v         

                       = − cos v

sin 270° = −1

 cos 270° = 0

Przykład nr 3

Znajdź wzór na cos 3x, w którym jest jedynie sin x i cos x.

Wykorzystujemy tożsamość cos (u + v) = cos u cos v − sin u sin v i podstawiamy 2x za u i x za v. 

cos (2x + x) = cos 2x cos x − sin 2x sin x

cos 2x = cos2x − sin2x       sin 2x = 2 sin x cos x

                           = (cos2 x − sin2 x)∙cos x − (2 sin x cos x)∙sin x

                      = cos3 x − sin2 x cos x − 2 sin2 x cos x

                      = cos3 x − 3 sin2 x cos x

Przykład nr 4

Rozwiąż równanie sin 2x + 2 sin x = 0 w przedziale 0 x < 2p.

              sin 2x + 2 sin x = 0

   2 sin x cos  x + 2 sin x = 0

         2 sin x (cos  x + 1) = 0

 

Wykorzystujemy tożsamość
sin 2x = 2 sin x cos x

 

Rozwiązaniami równania jest sin x = 0  i cos x = -1.

   sin x = 0

         x = 0 eđa p (0° eđa 180°)

         x = 0 lub p (0° lub 180°)

   cos x = −1

          x = p(180°)

Rozwiązania to 0 i p.   

Przykład nr 5

Rozwiąż równanie 7 cos2 x + 5 sin2 x + 6 sin 2x = 0

Najpierw wykorzystujemy tożsamość sin 2x = 2 sin x cos x.

   7 cos2 x + 5 sin2 x + 12 sin x cos x = 0

Równanie tego typu, z dwoma czynnikami sin lub cos w każdym wyrażeniu, można rozwiązać dzieląc wszystko przez cos2 x i zmieniając równanie na równanie z tg.


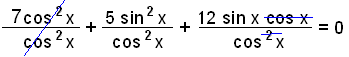
                                7 + 5 tg2x + 12 tg x = 0

To jest równanie kwadratowe ze współczynnikami a = 5, b = 12 i c = 7.



tg x












 

   tg x = −1 daje x = −p/4 + k∙p  (−45° + k∙180°)

   tg x = −7/5 nie daje całkowitej wielokrotności liczby p, lecz

         x ≈ −0,95 + k∙p  (54,5° + k∙180°)

Przećwicz powyższe przykłady, a potem zrób test nr 2.

PS Pamiętaj, aby regularnie wypełniać Twoją tabelkę wyników.