|
© 2009 Rasmus ehf og Jóhann Ísak Pétursson |
Funkcje I |
Drukuj |
Prezentacja nr 2
Wielomiany
Poniższe funkcje są przykładami wielomianów:
|
Stopień |
f(x) |
przykładowy wykres |
|
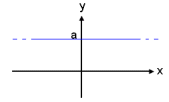
0 |
f(x) = a Stuðull: a Stała: a |
|
|
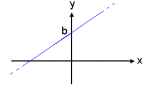
1 |
f(x) = ax+b Stuðlar: a og b Stała: a i b |
|
|
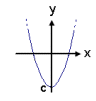
2 |
f(x) = ax2+bx+c Stuðlar: a, b og c Stała: a, b i c |
|
|
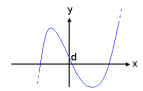
3 |
f(x) = ax3+bx2+cx+d Stuðlar: a, b, c og d Stała: a, b, c i d |
|
|
4 |
f(x) = ax4+bx3+cx2+dx+e Stuðlar: a, b, c, d og e Stała: a, b, c, d i e |
|
|
itd. |
||
Stałe a, b, c itp. są znanymi stałymi, które determinują kształt wielomianu. x jest zmienną, dla której możemy wybierać wartości. Najwyższa potęga x, która pojawia się w wielomianie, nazywana jest "stopniem" wielomianu. Wyrażenie o najwyższej potędze x piszemy najpierw, a następne w kolejności malejącej. Jeśli brakuje którejś z potęg x to znaczy, że współczynnik przy niej równy jest 0. Jeśli przy wyrażeniu nie stoi żaden współczynnik to znaczy, że współczynnik ten wynosi 1.
Przykład nr 1
Podaj stopień wielomianu oraz jego współczynniki:
f(x) = x5 − 2x3 + 4x − 5
Najwyższa potęga x wynosi 5, więc jest to wielomian stopnia 5. Nie ma x4 oraz x2 więc stałe przy nich wynoszą 0. Przy x5 nie ma żadnej widocznej stałej, więc wynosi ona 1. Możemy myśleć o wyrażeniu bez x jako o wyrażeniu z x0, bo jak wiadomo wszystkie liczby podniesione do potęgi 0 równają się 1. Teraz możemy przepisać ten wielomian i podać współczynniki.
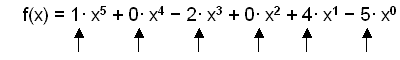
Współczynniki: 1, 0, -2, 0, 4 i
-5
Potęgi wielomianu są zawsze całkowite, dodatnie lub zero. Poniższe funkcje nie są wielomianami:
|
f(x) = x2
+ x + 1 + x−1
+ x−2 |
(ujemna potęga x) |
|
g(x) = x2
+ x + 1 + Öx |
(x jest pod pierwiastkiem) |
|
h(x) = x2
+ x + 1 + 2x |
(x jest potęgą) |
|
|
(x jest w mianowniku) |
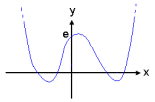
Jeśli spojrzysz na wykresy wielomianów powyżej to dostrzeżesz, że wielomian
stopnia 0 to pozioma prosta. Wielomian stopnia pierwszego ma wykres nachylonej
prostej. Wykres wielomianu stopnia drugiego nazywany jest parabolą. Ma jeden
punkt przegięcia. Wykres wielomianu stopnia trzeciego wygląda trochę jak
połączone dwie parabole, jedna otwarta do góry a druga do dołu. Może mieć dwa
punkty przegięcia. Wykres wielomianu czwartego stopnia przypomina trzy parabole
połączone razem, które mogą mieć maksymalnie 3
punkty przegięcia, itd. Wraz ze wzrostem stopnia wielomianu wzrasta również
możliwa liczba punktów przegięcia. Maksymalna liczba punktów przegięcia jest
zawsze o jeden mniejsza od rzędu wielomianu.
Wynika stąd również, że wielomian pierwszego stopnia przecina oś x tylko raz,
wielomian drugiego stopnia przecina oś x najwyżej dwa razy, trzeciego stopnia
najwyżej trzy razy itd. (przyjrzyj się ponownie
wykresom).
Wyraz stały (wyraz, przy którym nie stoi x) mówi nam gdzie wykres przecina oś y. To wynika z tego, że x=0 na osi y i jeśli wstawimy x=0 do równania to pozostanie nam w równaniu tylko wyraz stały.
f(x) = 2x3 + 3x2 + 4x + 6 to
f(0) = 2∙03 + 3∙02 + 4∙0 + 6 = 6
Punkt (0, 6) to punkt, w którym wykres przecina oś y.
Wszystkie punkty na osi x mają y równe zero, zatem możemy znaleźć punkt gdzie wykres przecina oś x przez wstawienie y=0 i rozwiązanie równania na x. y=f(x)=0.
Przykład nr 2
Znajdź punkty gdzie wielomian f(x) = 2x + 4 przecina osie x
oraz y.
|
punkt przecięcia z osią x: 4 |
Wyraz stały: 4 |
|
2x + 4 = 0 |
Wstaw f(x) =0. |
|
x = −4/2 = −2 |
Rozwiąż na x. |
|
punkt przecięcia z osią x: -2 |
|
Przykład 3
Znajdź miejsca przecięć wielomianu f(x) = x2 − 2x z
osiami x oraz y.
|
punkt przecięcia osi y: 0 |
Wyraz stały: 0. |
|
x2 −
2x = 0 |
Wstaw f(x) = 0. |
|
x (x − 2) = 0 |
Wyłącz czynnik przed nawias i rozwiąż. |
|
punkt przecięcia osi x: 0 oraz 2 |
|
Przykład nr 4
Znajdź punkty przecięcia wielomianu f(x) = (x − 1)(x − 2)(x − 3) z osiami x i y.
Przyglądając się równaniu możemy zauważyć, że jeśli przemnożymy przez siebie nawiasy to wyraz wolny wielomianu będzie wynosić -6.
(x − 1)(x − 2)(x − 3) = (x2 − 2x − x + 2)(x − 3)
= (x2 −3x + 2)(x − 3)
= x3 − 3x2 − 3x2 + 9x + 2x − 6
= x3 − 6x2 + 11x − 6
Innym, łatwiejszym sposobem na znalezienie punktu przecięcia jest obliczenie f(0) bez wymnażania nawiasów przez siebie.
f(0) = (0 − 1)(0 − 2)(0 − 3) = −6
Przecięcie osi y jest dla y = −6.
Aby dowiedzieć się gdzie wielomian przecina oś x musimy rozwiązać równanie:
(x − 1)(x − 2)(x − 3) = 0
Jedyną możliwością, aby to mnożenie dało wynik 0, jest aby jeden z nawiasów był równy 0. To ma miejsce gdy x = 1, 2 lub 3. Zatem widzimy, że wykres
przecina oś x gdy x=1,
x =2 i x=3.
Przykład nr 5
Sprawdźmy, czy punkty (1,6) i (2,8) leżą na wykresie funkcji f(x) = x2 + 4x + 1.
|
f(1) = 12
+ 4∙1 + 1 |
Oblicz wartość funkcji dla x równe 1. |
|
= 1 + 4 + 1 = 6 |
|
(1, 6) leży na wykresie.
f(2) = 22 + 4∙2 + 1
= 4 + 8 + 1 = 13
(2, 8) nie leży na wykresie.
Przykład nr 6
Znajdź równanie wielomianu stopnia pierwszego (linia prosta), który przecina punkty (1,1) i (2,3).
Funkcja
f(x) = ax + b
|
f(1) = a∙1 + b = 1 prowadzi do równania a + b = 1 |
Wstaw 1. |
|
f(2) = a∙2 + b = 3 prowadzi do równania 2a + b = 3 |
Wstaw 2. |
|
f(2)
− f(1) = (2a + b) − (a + b) = 3 − 1 |
Rozwiąż układ równań a + b = 1 |
Równanie wielomianu (prostej) to f(x) = 2x − 1.
Przykład
nr 7
Znajdź równanie wielomianu stopnia drugiego (parabola), który przechodzi przez punkty (0,6), (1,0) i (3,0).
Weź funckję f(x) = ax2 + bx + c i oblicz a, b i c.
(0, 6) to punkt przecięcia osi y, zatem c = 6.
f(1) = a∙12
+ b∙1 + 6
= a +
b + 6 = 0
|
f(3) = a∙32
+ b∙3 + 6 = 0 |
|
Uprość równanie przez podzielenie całości przez 3. |
f(3) = f(1) = 0
3a + b + 2 = a + b + 6
3a − a + b − b = 6 − 2
2a = 4
a = 2
f(1) = 2 + b + 6
= 0
b = −2 − 6 = −8
Zatem wielomian to f(x) = 2x2 − 8x + 6
Przećwicz powyższe przykłady, a
potem zrób test nr 2.
PS Pamiętaj, żeby regularnie wypełniać Twoją tabelkę wyników.