© 2007 Rasmus ehf og Jóhann Ísak
© 2007 Rasmus ehf og Jóhann Ísak |
Funksjoner I |
Vi har likningen y = 2x + 4.
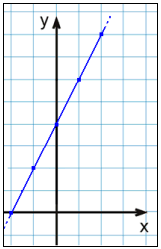
Først lager vi en verditabell hvor vi regner ut y-verdiene for x-verdiene vi har valgt. Når vi merker av disse punktene i et koordinatsystem, ser vi at de ligger på en rett linje. Vi trekker opp en strek mellom punktene.
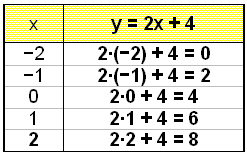 |
 |
Dette er det veldig lett å gjøre med en grafisk
kalkulator. Hvis man har Casio kalkulator, velger man TABLE i menyen.


Så skriver vi 2x + 4 i menyen som kommer frem. Nå
ser du Y1 = 2x + 4 på skjermen.
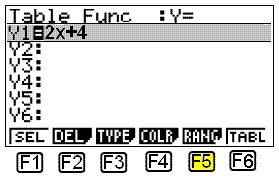
Nå må vi bestemme hvilke x-verdier vi vil bruke. For å gjøre dette, velger vi ”RANG” ved å trykke F5. Da får vi dette opp på skjermen:
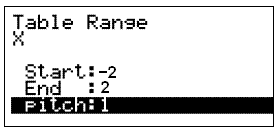
Vi velger x-verdiene fra -2 til 2. Ved hjelp av “pitch” kan vi bestemme hvor mye det skal være mellom hver x-verdi. I dette tilfellet lar vi den være 1, og trykker EXE. Da vil det altså være 1 mellom hver x-verdi.
Dette er knappene du må trykke på:
![]()
Dette fører oss tilbake til det forrige skjermbildet, hvor vi velger TABL, ved å trykke F6. Da får vi frem verditabellen.
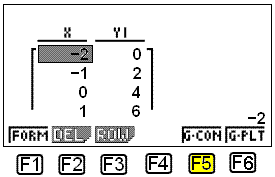
Vi kan tegne grafen ved å velge G-CON ( F5 ).
Vi kan også bruke
programmet EXCEL til å lage verditabellen og tegne en graf.
![]()
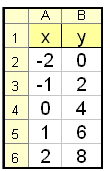
I EXCEL skriver vi inn tallene −2 og −1 i cellene A2 og A3 (se EXCEL-tabellen ovenfor). Vi kan automatisk fylle inn resten av kolonnen ved å merke av A2 OG A3, og deretter venstreklikke i det svarte krysset nederst i et av hjørnene, og dra nedover til A6. I B2 skriver vi formelen =2×A2 + 4, som vi kan kopiere nedover på samme måte som med x-verdiene.
Vi kan tegne grafen ved å markere tallene i de to kolonnene, og trykke på graf-knappen (1). |
|
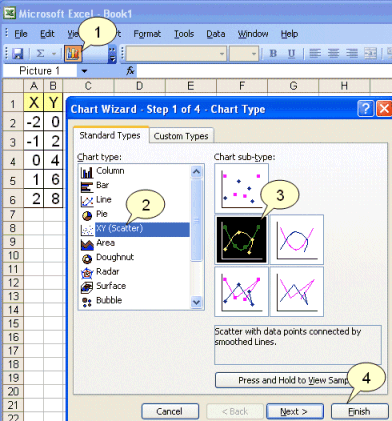 |
Vi velger ”punktdiagram (xy)” (2) |
og velger så en av grafene (3) |
|
| før vi trykker ”Fullfør” (4) |
Så kan vi gjøre forandringer på grafens utseende ved å klikke på det vi vil forandre med høyre museknapp.
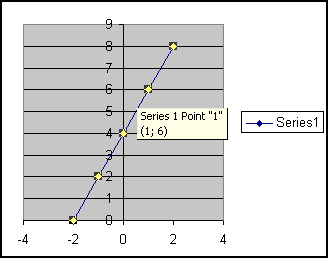
Nå skal vi se på noen flere eksempler.
Lag en verditabell og tegn de følgende grafene
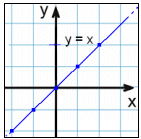
Graf x = y |
|
 |
 |
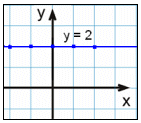
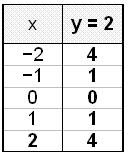
Graf y = 2 |
|
 |
 |
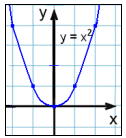
Graf y = x2 |
|
 |
 |
Graf y = 2x |
|
 |
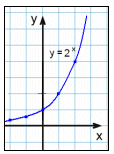 |
Nå skal vi se på noen oppgaver som ikke kan løses på den denne måten. I disse oppgavene kan vi ikke bruke tabellfunksjonen på kalkulatoren, fordi de ikke er skrevet som y=…
Eksempel 3
Graf x = 2
Det eneste vi får ut av dette, er at x er 2. Når vi lager en verditabell, må vi ha x lik 2 hele veien. y kan ha en hvilken som helst verdi, men vi har valgt −2, −1, 0, 1 og 2. Her kan du se vår verditabell.
|
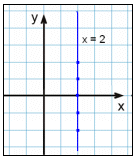 |
Resultatet er en vertikal linje gjennom punktet 2 på x-aksen.
Eksempel 4
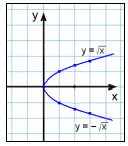
Nå skal vi se på forholdet y2 = x.
Når vi løser likningen for y får vi to svar.
y = ±√x
Med andre ord finnes det to verdier av y for hver x vi velger. Dessuten kan vi bare velge positive verdier for x, fordi det ikke er mulig å regne ut kvadratroten av et negativt tall. Under kan du se verditabellen og grafen.
X |
Y = ±√x |
 |
-1 |
Umulig | |
0 |
0 | |
1 |
±1 | |
2 |
±√2 |
|
3 |
±√3 | |
Eksempel 5
Nå skal vi se på likningen x2 + y2 = 4.
Løsningen til y.
x2 + y2 = 4
y2 = 4 − x2
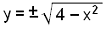
Også denne gangen får vi to y-verdier for hver x-verdi vi velger. Vi ser også at x-verdiene vi velger må være innenfor intervallet [−2, 2]. Ellers ville vi få et negativt tall under kvadratroten. Under ser vi verditabellen og grafen.
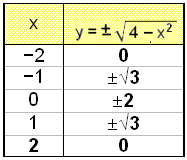 |
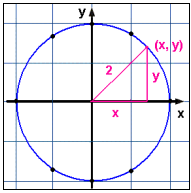 |
Når vi setter punktene inn i et koordinatsystem, ser vi at de er i en sirkel, med sentrum i origo (0, 0). Radius til sirkelen er 2.
Dette resultatet er lett å forklare, fordi x2 + y2 = 4 faktisk er Pythagoras regel for en rettvinklet trekant, der hypotenusens lengde er 2, og de andre x og y. Disse eksemplene viser at noen likninger som gir en sammenheng mellom x og y, bare har en y-verdi for hver x som vi velger, og noen likninger har mer enn en y for hver.
Likninger som forbinder en y med en x er veldig viktig i vitenskapen, og
kalles funksjoner. Man sier at ”y er en funksjon av x”, og skriver dette
y = f(x). Dette leser vi: ”y er lik f av x”.
Når vi ser på grafen til en funksjon, ser vi at vertikale linjer bare krysser grafen en gang.
Dette ser vi hvis vi ser på grafene i eksemplene som vi allerede har sett på.
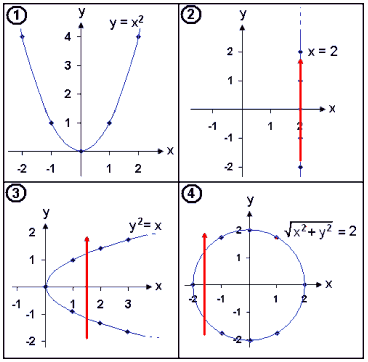
Den røde, vertikale linjen krysser grafene 2, 3 og 4 på to eller flere
steder. Dette viser at disse ikke er funksjonsgrafer.I
eksempel 1 vil en vertikal linje uansett bare krysse grafen en gang. Dette er
funksjonsgrafen til likningen y = x2.
I tillegg til å skrive likningen som y = x2, kan vi skrive den som f(x) = x2, hvor y = f(x). Vi bruker f(x) istedenfor y for å vise at y-verdien kommer an på x-verdien, altså at y ”er en funksjon av x”.
Hvis vi velger x = 2, kan vi regne ut y slik: y = 22 = 4.
Med funksjonsspråk kan vi si at f av 2 er lik 4.
Med funksjonsnotering kan man skrive: f(2) = 22 = 4.
Eksempel 6
Gitt funksjonen Finn
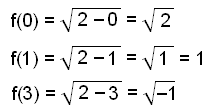 |
Vi setter inn verdiene 0, 1 og 3 i likningen istedenfor x, og regner ut funksjonsverdien (y-verdien) I hvert tilfelle. |
Umulig |
|
På samme måte kan vi sette inn bokstaver i funksjoner.
f(a) = a3 + a2 og f(a2) = a6 + a4 og f(a+1) = (a+1)3 + (a+1)2.
Eksempel 7
Gitt funksjonen f(x) = x2. finn f(a), f(2a), f(a+1) og f(a+b).
f(a) = a2
f(2a) = 4a2
f(a+1) = (a+1)2 = a2 + 2a + 1
f(a+b) = (a+b)2 = a2 + 2ab + b2
Prøv test 1 i
Funksjoner 1.
Husk å fylle inn
resultatet i sjekklisten din.