© 2010  Rasmus ehf  og Jóhann Ísak

Vektorer

Introduksjon 4  

 Skalarprodukter og vinkelrette vektorer

Hvordan kan vi finne vinkelen mellom to vektorer? Cosinussetningen er et bra hjelpemiddel, fordi den lar oss regne ut vinkelen mellom to nærliggende sider i en trekant (se Trektanter Introduksjon 3). Vi kan lage en trekant med vektorene , og - (se Vektorer Introduksjon 1), men la oss først se nærmere på dette ved hjelp av en tegning.

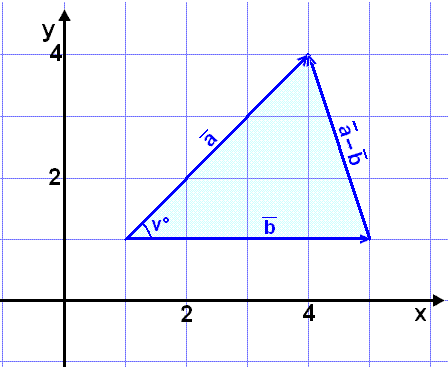
Vi kunne ha lest av koordinatene direkte, men vi bruker heller generelle verdier.

Cosinussetningen er som følger:

    c² = a² + b² − 2∙b∙a∙cos C

Her representerer || siden a i formelen, || siden b, | - | siden c. Vinkelen C tilsvarer v° hos oss. Vi setter cosinussetningen med våre variabler.

| - |² = ||² + ||² - 2∙||∙ ||∙cos v°

Nå kan vi bruke avstandsformelen til å finne lengden til vektorene.

    (x_a − x_b)² + (y_a − y_b)² = x_a² + y_a² + x_b² + y_b² − 2∙||∙ ||∙cos v° 

Vi ganger ut parentesene på venstre side:

   x_a² − 2x_ax_b + x_b² + y_a² − 2y_ay_b + y_b²

Vi fjerner ledd som finnes på begge sider av likhetstegnet, og står igjen med:

   − 2x_ax_b − 2y_ay_b = − 2∙||∙ ||∙cos v° 

Vi deler begge sider på -2.

Vi har nå skalarproduktet på begge sider av likhetstegnet. Vi kan altså regne ut skalarproduktet på to forskjellige måter:

    Skalarproduktet til og = x_ax_b + y_ay_b  og skalarproduktet til og = ||∙ ||∙cos v° 

Skalarproduktet kan også skrives som multiplikasjon av to vektorer:
∙ = x_ax_b + y_ay_b  og  ∙ = ||∙ ||∙cos v° 

Eksempel 1

Vi skal regne ut skalarproduktet til vektorene og på bildet under, på begge måtene vi har lært.

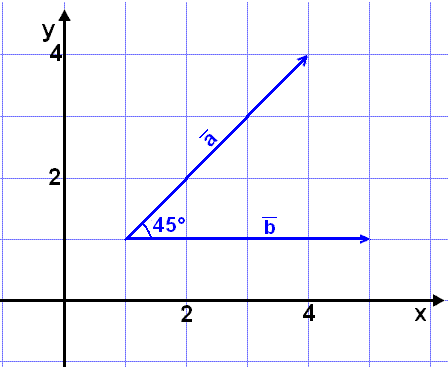
Vi kan lese av vektorenes koordinater, og lengden til . Lengden til må vi regne ut.

Utregning ved hjelp av koordinatene:

Utregning ved hjelp av vektorenes lengder og cosinus til vinkelen mellom dem:

|| =

|| = 4

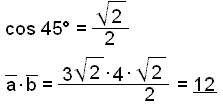
    x_ax_b + y_ay_b = ||∙ ||∙cos v° 

Hvis vi deler med ||∙| | på begge sider, får vi:

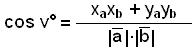Om vi deretter bruker avstandsformelen for   og , får vi:

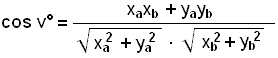Eksempel 2

Vi skal regne ut vinkelen mellom vektorene

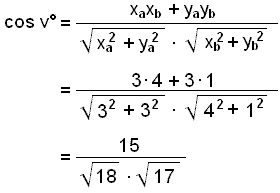
              ≈ 0,8575

           v° ≈ cos⁻¹ 0,8575 ≈ 31°

Eksempel 3

Hvilken vektor er like lang som vektor			og vinkelrett med den?
Vi kaller vektoren		og skriver opp skalarproduktet.

   x_ax_b + y_ay_b = ||∙ ||∙cos 90° 

Nå er cos 90° = 0, så vi får følgende likning:

   x + 2y = 0

Vi har at ||²  = x² + y² = 5.

Vi setter likningene x + 2y = 0 og x² + y² = 5 inn i hverandre.

    x = −2y  og x² = 5 − y²

   x² = 4y² = 5 − y²

 5y² = 5

   y² = 1

    y = ±1

Hvis y = 1, er x = −2 og hvis y = −1, er x = 2.

Vi har to muligheter,

Vi tegner opp vektorene.

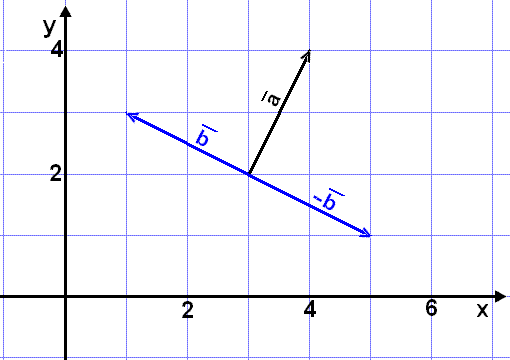
Eksempelet over viser at vi kan rotere en vektor 90° ved å bytte om koordinatene og endre fortegn på en av dem.

Regelen over gjelder for like lange vektorer, eller om vi roterer den samme vektoren 90° til høyre eller venstre. Fordi cos 90º = 0, gjelder følgende regel:

Dette gjelder også den andre veien:

Eksempel  4

En trekant har hjørnepunktene A = (–3, –4), B = (17, –12) og  C = (5, 16). Vi skal regne ut vinklene.

Vi begynner med å finne vektorer som representerer sidene i trekanten.

Vi trenger ikke å regne mer. Vektorene og danner en rett vinkel, og er like lange. Trekanten er rettvinklet og likebent. Da må vinklene være

A = 90º, B = 45º og C = 45º.

Eksempel 5

En trekant har hjørnene A = (–3, –3), B = (21, 7) og  C = (4, 14).

a)  Vi skal regne ut vinkel A.

Først regner vi ut vektorene og .

Deretter finner vi ut hvor lange de er.

Nå kan vi regne ut vinkelen mellom og .

Her multipliserer vi med 2 både over og under brøkstreken.

b)  Nå skal vi regne ut høyden fra C til siden AB.

         sin A = h/||

         h = || · sin A

            = 13·2·2/₂

            = 13

c)   Vi skal finne vektoren , som representerer høyden fra C til siden AB.

Vektoren er vinkelrett med og dobbelt så lang. Vi kan derfor finne vektoren  ved å rotere 90º og dele koordinatene på 2.

Øv på eksemplene, og regn deg gjennom Test 4 i Vektorer.

Husk å fylle ut sjekklisten underveis.