© 2010  Rasmus ehf    og Jóhann Ísak

Vektorer

Introduksjon 3 

Vektorer i et koordinatsystem

Eksempel 1

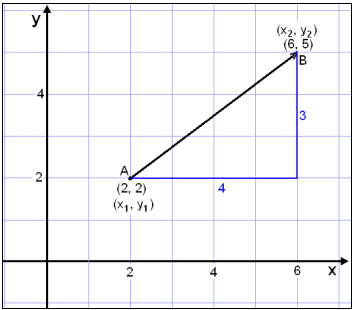
Vi tenker oss at punktet A har koordinatene(2, 2) og punktet B har koordinatene (6, 5) (se bildet). Koordinatene til vektoren er:

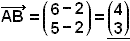
Vi kan bruke avstandsformelen til å regne ut avstanden mellom A og B, og dermed lengden av vektoren . Formelen ser slik ut:

Sett koordinatene inn i formelen:

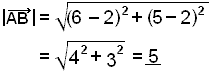
Som vi ser, havner vektorens koordinater under rottegnet. Dette er ingen tilveldighet, da vektoren er like lang som hypotenusen til den rettvinklede trekanten på bildet.

Formelen for lengden av en vektor er som følger, når vektoren begynner i punktet A = (x₁, y₁) og slutter i punktet B = (x₂, y₂). 

Hvis vi kjenner koordinatene til vektoren

,

gjelder følgende formel:

Eksempel 2

men bare halvparten så lang (se bildet).

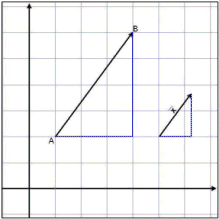
Trekantene på bildet er formlike, så || = t∙||. Tallet t er forholdet mellom trekantenes sider, eller  = . Vi kan derfor finne koordinatene slik:

Hvis vektorene og er parallelle, gjelder følgende formel:

= t∙

Eksempel 3

Er vektorene   og parallelle?

Hvis vektorene er parallelle, finnes det et tall t slik at = t∙ og = r∙ . Vi kan regne ut tallene t og r ved hjelp av x- koordinatene, og kontrollere om likningen også gjelder for y - koordinatene.

= t∙

   3 = t∙13½ gir t = ³/13½ =²/9

   4 = t∙18 gir også t = ⁴/18 = ²/9

vektorene og er parallelle.

= r∙

  3 = r∙6 gir r = ½

  4 = r∙9 gir derimot r = ⁴/9

Vektorene og er ikke parallelle (da kan heller ikke og være parallelle).

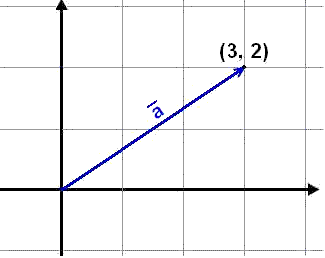
Vektoren på bildet over har koordinatene . Startpunktet er (0, 0), og sluttpunktet er (3, 2). Det vil si at vektoren har samme koordinater  som sluttpunktet, noe som gjelder for alle vektorer som begynner i origo.

Eksempel 4

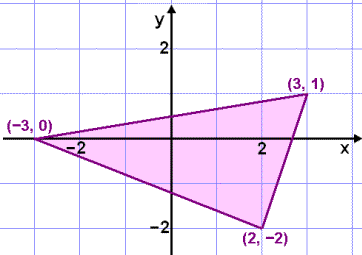
På bildet over ser vi en trekant som vi skal flytte med vektoren .

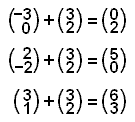
Vi har nå vektorkoordinatene for de nye hjørnepunktene. Bildet under viser forflytningen.

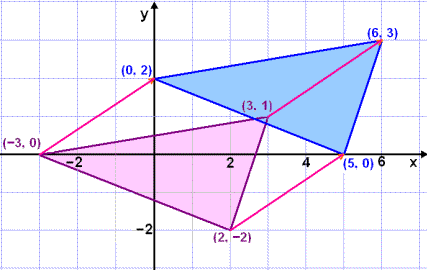
Eksempel 5

Nå skal vi bruke vektorer til å finne midtpunktet på linjen AB når A = (1, 2) og B = (4, 3).

Vi kaller koordinatsystemets midtpunkt O, og midtpunktet på AB kaller vi M. Vi får følgende likning:

    = + ½∙

Vektoren har de samme koordinatene som midtpunktet vi leter etter. Vektoren har samme koordinater som punkt A, og vi må legge til halve  . Tegn en tegning for å visualisere vektorene. Regn med vektorkoordinatene.

Først finner vi koordinatene til vektoren .

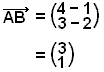
Regn deretter ut .

    = + ½∙

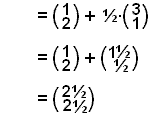
Koordinatene til punktet M er de samme som for vektoren , eller (2½, 2½).

Vi kan gjøre det lettere for oss selv ved å lage en formel for å regne ut midtpunktet på en hvilken som helst linje AB.

2 = + ½∙ + - ½∙

Vi kan si at midtpunktet på en linje er gjennomsnittet av de to endepunktene på linjen. Når vi bruker vektorkoordinater, regner vi gjennomsnittet av x - koordinater og y - koordinater for seg.

Eksempel 6

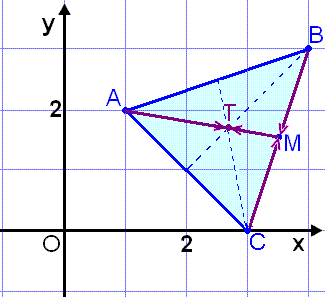
En trekant har hjørner i A = (1, 2), B = (4, 3) og C = (3, 0). Vi skal regne ut lengden på linjen fra Vinkel A til midtpunktet på linjen BC (medianen).

Først finner vi midtpunktet på BC ved hjelp av formelen over.

Vi kaller midtpunktet M og regner ut (se bildet)

= ½∙ + ½∙

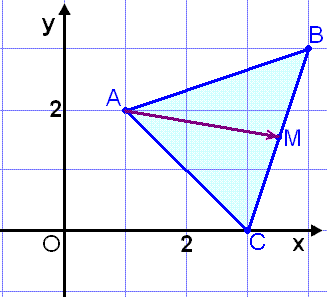Midtpunktet på BC har koordinatene M = (3½, 1½).

Nå regner vi ut koordinatene til vektoren .

Vi kan deretter regne ut lengden til medianen, .

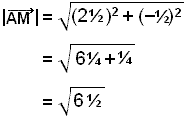
           ≈ 2,55

Skjæringspunktet mellom de tre medianene i en trekant gir oss trekantens tyngdepunkt (se punkt T på bildet). Vi kan finne formelen for å regne ut koordinatene til T på samme måte som da vi fant regelen for gjennomsnittspunkter. Vi bruker vektorene for trekantens hjørnepunkter for å komme til punktet T, og legger likningene sammen.

I Trekanter Introduksjon 2 lærte vi at medianene i en trekant skjærer hverandre i et punkt, og deler hverandre i forholdet ²/1. Det vil si at vektoren   er dobbelt så stor som . Det vil si at
= ∙ og = −∙. Vi kan derfor sette opp disse tre likningene:

= + ∙ 

= + ½∙ - ∙

= - ½∙ - ∙

Vi legger dem sammen, og får følgende likning:

3 = + +

Husk å finne finne gjennomsnittet av x - koordinater og y - koordinater for seg.

Vi kan med andre ord finne skjæringspunktet til medianene, eller tyngdepunktet T, ved å regne ut gjennomsnittet av vektorene fra hjørnepunktene. Denne formelen er en utvidelse av regelen for gjennomsnittspunkter.

Hadde vi vist at dette gjelder fra de tre hjørnepunktene, kunne vi også bevist at medianene må skjære hverandre i et punkt, og dessuten regelen om at at medianene skjærer hverandre slik at forholdet mellom lengdene er ²/1.

Eksempel 7

Vi skal regne ut tyngdepunktet T (skjæringspunktet for medianene) på en trekant med hjørnepunktene A = (1, 2), B = (4, 3) og C = (3, 0) (se bildet).

Tyngdepunktet er T = (2, 1).

Øv på eksemplene, og regn deg gjennom Test 3 i Vektorer.

Husk å fylle ut sjekklisten underveis.