© 2010  Rasmus ehf    og Jóhann Ísak

Vektorer

Introduksjon 2  

Vektorens komponenter

Når vektoren er delt inn i to andre vektorer og slik at  + = , sier vi at dette er komponentene til vektor . Se bildet under.

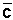Vektorer deles ofte inn i vannrette og loddrette vektorer, fordi disse komponentene er viktige for eksempel i kraftutregninger i fysikk. Generelt kan man dele opp vektoren slik at komponentene er parallelle med en hvilken som helst vektor. La oss se på et kjent eksempel (se bildet under). Vi ønsker å skrive vektoren ved hjelp av vektorene og , med andre ord dele opp vektor i komponenter som er parallelle med vektorene og .

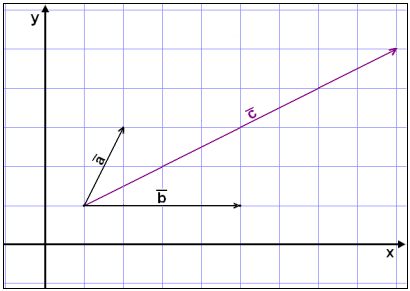
Legg en vektor til den som allerede er der, og deretter en og en halv vektor .

Nå ser vi at komponentene er 2 og 1½. Vi kan dele opp alle vektorer i komponenter som er parallelle med to vektorer og , som ikke er parallelle med hverandre, når ingen av vektorene er en nullvektor (har lengden 0).

   = r∙+ t∙

Fremgangsmåten er å finne tallene t og r (komponentene) slik at likningen over blir riktig.

Eksempel 1

Nå skal vi dele opp vektorene , og fra bildet i vannrette og loddrette komponenter. Vi bruker en vannrett vektor med lengden 1 (1 rute) og en like lang loddrett vektor. Disse vektorene kalles enhetsvektorer, og betegnes med og .

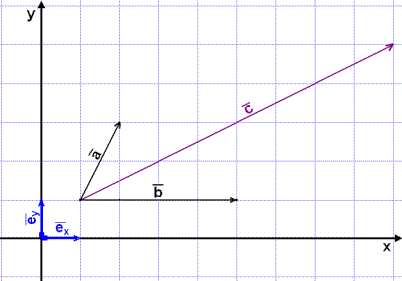
Vi begynner med å dele opp vektoren.

Vi ser av bildet at = + 2.

Som vi ser, er det lett å regne ut komponentene for de to andre vektorene. Vektor går 4 ruter til høyre, og ingen ruter opp. Vektor   går 8 ruter til høyre og 4 opp.

= 4 og = 8 + 4.

Eksempel 2

En kraft på 200 N er rettet oppover med 25° i forhold til planet. Hva blir kraftens effekt i planets retning og rett oppover?

Vi tegner opp en tegning for å få bedre oversikt over problemet.

Nå kan vi bruke trigonometriske regler for å regne ut || og ||

En vannrett komponent som den vi regnet ut over, kalles x - komponenten, fordi det er komponenten i x - retning. På samme måte kan vi kalle den loddrette komponenten for y - komponenten.

Vi har nå formlene for å finne x og y - komponentene:

Eksempel 3

Vektor har lengden 3 og retning 20° i forhold til planet. Vektor har lengden 4 og retning 40° i forhold til planet. Vektor har lengden 5 og retning 70° i forhold til planet. Dette gir oss at vinkelen mellom   og er 20°, og vinkelen mellom og er 30°. Vi skal dele opp vektor i komponenter som er parallelle med og , men først tegner vi opp vektorene.

Vi må nå finne vektorene r∙ og t∙ som til sammen blir vektor . Når vi tegner dem inn, får vi en trekant (blå på bildet) som har vinkelen 30° mellom vektorene og , og 20° mellom  og . Den tredje vinkelen må derfor være 180°− 30°− 20° = 130°. Vi kjenner alle vinklene i trekanten, og en side  med lengden 4 (||= 4). Vi kan derfor bruke sinussetningen.

Her bruker vi sinussetningen og multipliserer begge sider med sin 30°.

På samme måte finner vi t∙||

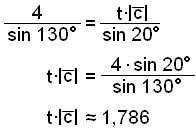
Nå har vi funnet trekantens sider, og skal finne r og t. Vi begynner med r.

   r∙|| 2,611

      r∙3 2,611

         r ^2,611/3 0,87

Regn deretter ut t.

    t∙|| 1,786

      t∙5 1,786

         t ^1,786/5 0,36

Komponentene er som følger:

   0,87∙ + 0,36∙

Fra Eksempel 3 ser vi at vi kan bruke sinussetningen til å dele en vektor opp i komponenter som er parallelle med to andre vektorer. Det eneste vi trenger er de tre vektorenes retning og lengden på vektoren som vi vil dele opp. Denne metoden er så viktig at vi setter den i en ramme.

Det er mye lettere å dele opp vektorer når de er i et koordinatsystem. I Eksempel 1 introduserte vi enhetsvektorene, og .

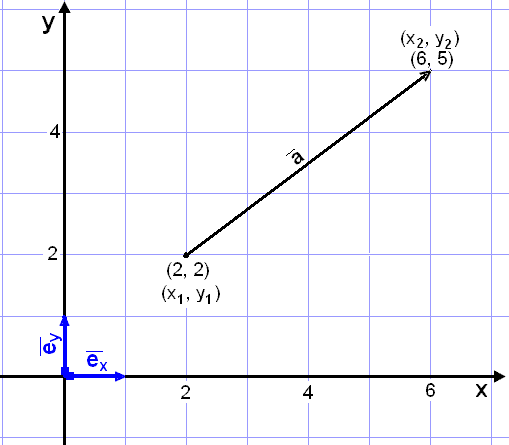
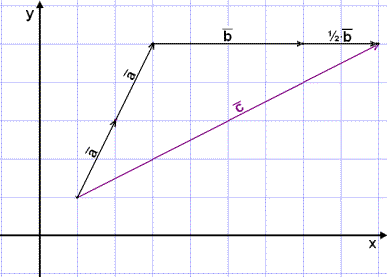
Vi kan dele opp vektor på bildet ovenfor på samme måte som i Eksempel 1. Resultatet er som følger:

   = 4 + 3

For å komme fra startpunktet (2, 2) til endepunktet (6, 5) må vi flytte oss fire ruter (4) til høyre og tre ruter (3) opp. Dette gir oss at x - komponenten av  er 4, og y - komponenten er 3. Vi kan også finne disse ved å regne ut differansen mellom koordinatene i startpunkt og endepunkt.

   6 − 2 = 4 og 5 − 2 = 3

Vi kan som kjent plassere en vektor hvor som helst i et koordinatsystem. Det lønner seg ofte å plassere vektoren i origo (0, 0). Vektorens endepunkt blir i dette tilfellet (4, 3), og vi kan si at vektoren har koordinatene

    = (4, 3)

Dette er en enklere og riktigere måte å beskrive en vektor, som tross alt er er uavhengig av posisjonen i et koordinatsystem. Vektoren (4, 3) beskriver en vektor som strekker seg 4 enheter til høyre og 3 enheter opp.

Problemet med skrivemåten er at den kan skape uklarhet i om det dreier seg om vektorkoordinater eller punktkoordinater. Selv om noen lærebøker gjør det slik, er det vanligere å skrive vektorer slik:

Likningen for koordinatene til en vektor er som følger:

Eksempel 4

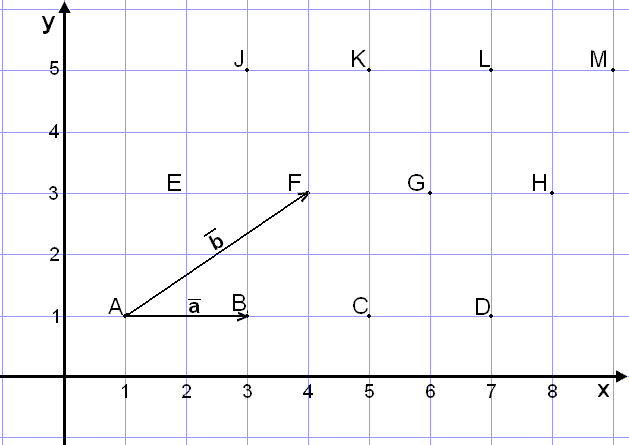
a)   Nå skal vi regne ut koordinatene til vektoren =

  Her har vi kun en forflytning på to ruter til høyre. Siden det ikke er noen loddrett forflytning,
må y - koordinatet være 0.

   Vi kan også bruke likningen endepunkt (B) − startpunkt (A).

   Vi har A = (1, 1) og B = (3, 1).

b)   Nå skal vi finne koordinatene til =

       Vi har A = (1, 1) og F = (4, 3).

c)   Hvordan regner vi ut koordinatene til vektoren + ? Vi ser at om vi kobler sammen vektorene og , havner vi i punktet G. Da har vi forflyttet oss 5 ruter til høyre og 2 opp. V i kan også regne det ut slik:

d)  Nå skal vi se på koordinatene til vektoren   - . Hvis vi snur vektoren og kobler den til , får vi vektoren, , som flytter oss en rute til venstre og to ned. V kan også regne det ut ved hjelp av koordinatene.

e)   Til slutt skal vi regne ut koordinatene til vektoren   + 2. Hvis vi dobler vektor og legger til vektor , havner vi i punktet M. Vi har forflyttet oss 8 ruter til høyre og 4 opp. Regnet ved hjelp av koordinatene:

I eksempelet over har vi funnet regler som vi kan bruke når vi adderer, subraherer eller multipliserer med en konstant når vektoren er på koordinatform.

Gitt vektorene og på formen:

og

Da gjelder følgende regler:

Eksempel 5

Nå skal vi løse et problem som ligner på Eksempel 3. Denne gangen bruker vi et koordinatsystem, og vi trenger ikke å bruke trigonometri.

Gitt vektorene , og med koordinatene

  og

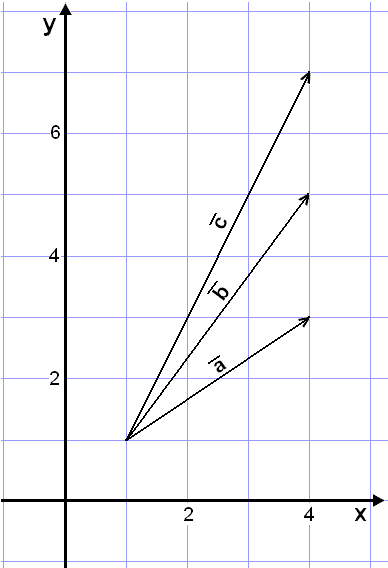
Vi skal nå dele opp vektoren i komponenter parallelle med vektorene og slik at følgende likning gjelder:   

= r∙ + t∙

Vi regner med koordinatene:

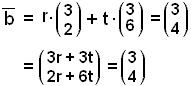
Det gir oss to likninger med to ukjente variabler.

   x-koordinatene gir likningen 3r + 3t = 3 eller r + t = 1 og

   y-koordinatene gir likningen  2r + 6t = 4 eller r + 3t = 2

Vi kan løse likningssystemet ved å trekke x - likningen fra y - likningen.

     r + 3t = 2

     −r − t = −1

           2t = 1

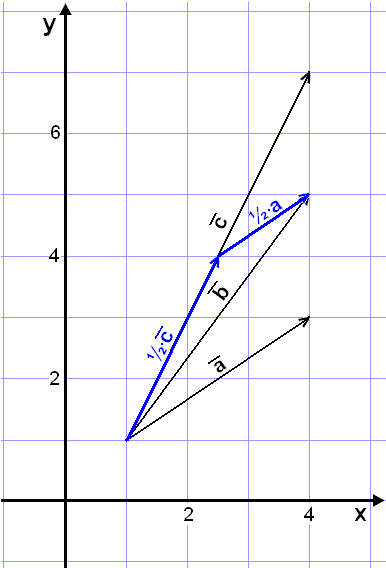
             t = ½  og  r = ½

Oppdelingen blir da = ½∙ + ½∙  som på bildet under.

Øv på eksemplene, og regn deg gjennom Test 2 i Vektorer.

Husk å fylle ut sjekklisten underveis.